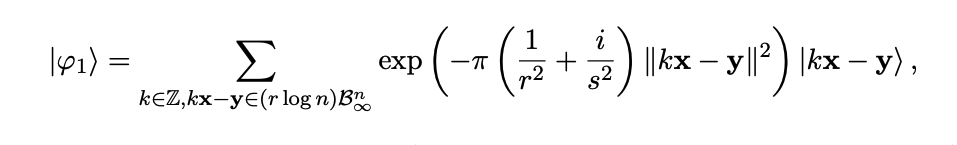背景
2024/04/10にIACRに”Quantum Algorithms for Lattice Problems”という論文が投稿された。このタイトルを読んだ多くの暗号研究者は震えたことだろう。
というのも、耐量子暗号や完全準同型暗号のセキュリティベースとなっている格子暗号(Lattice-based Cryptograpy)には耐量子性があると信じられてきた。これは、量子アルゴリズムによって格子の中からあるベクトルを見つける「LWE問題」という問題を解くことは困難であるという仮定に基づいた暗号である。
ここまで言われると多くの人が気付くと思うが、この論文のタイトルは、その格子暗号に真っ向から挑戦状を叩きつけるものである。2000年頃に「コンピュータで有限時間で素因数分解できました」という人が現れたことを想像すると、恐怖である。
この記事では、論文でなにをやってなにができるのかを整理する。
簡潔に結論から先にいうと、「RSA-512が解けたがRSA-2048は解けていない」みたいなイメージである。
論文の概要 (Abstract)
この論文では、ある特定のモジュラス・ノイズ比率におけるLWE問題を解く多項式時間量子アルゴリズムを提案する。ある方式の組み合わせによって、GapSVP問題とSIVP問題を解くためのアルゴリズムが得られる。(この時点で、まずいくつかの前提条件が存在していることに注意)
アルゴリズムの構築において、主に
- 複素分散ガウス関数
- 複素ガウスウィンドウを利用したウィンドウ量子フーリエ変換
の2つの手法を組み合わせることでLWEを解くための量子アルゴリズムを得ることができる。
主な結果 (1.1 Main results)
Let us remark that the modulus-noise ratio achieved by our quantum algorithm is still too large to break the public-key encryption schemes based on (Ring)LWE used in practice. In particular, we have not broken the NIST PQC standardization candidates.
論文 pp.3 1.1 Main resultsより引用
上記の引用によると、この論文で解けた設定は、NIST PQC標準化候補で提案されているような実用的なアルゴリズムには程遠い。そのため、格子暗号が耐量子性を破られたとはまだ到底言い難いことに注意したい。
技術の概要 (1.3 Overview of our algorithm for solving LWE)
このアルゴリズムでは量子フーリエ変換(QFT)、複素ガウスウィンドウ、そして他の標準的な量子計算ツールをもとに構成されている。しかし、これらの組み合わせは非常に複雑である。
具体的には、9つのステップからなる。それぞれのステップ実行とともに線形方程式を得ることができる。9ステップの実行後、フルランク線形方程式が得られ、ガウス消去法によってLWEシークレットとエラーが計算される。
Step1は以下の通りである。ある暗号文
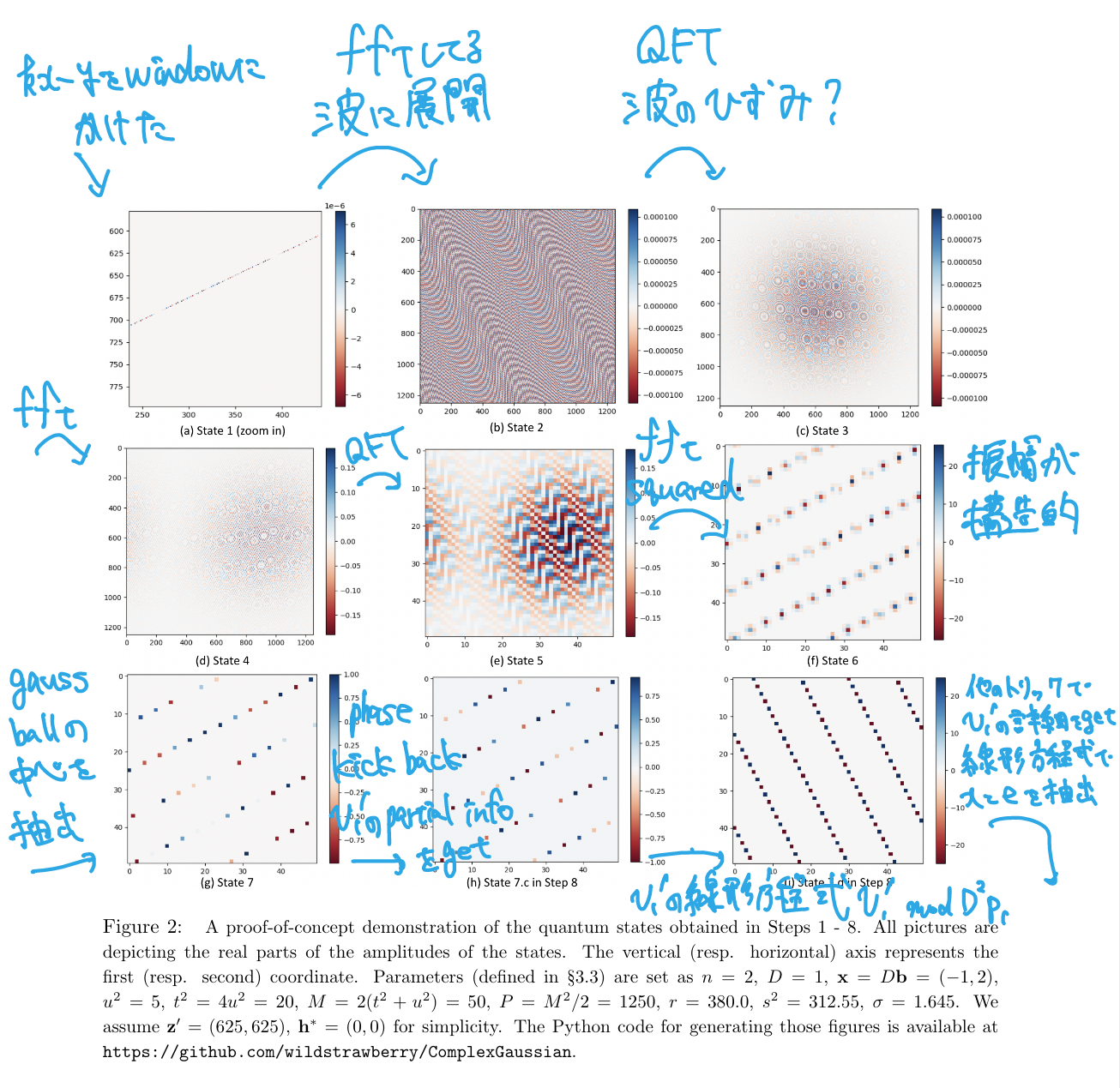
こういう式があと8回ほど続くが、ここでは割愛する。下に、各ステップ後の状態を可視化したグラフを示している。State iはStep i実行後の状態である。Step6を終えたあたりで振幅が構造的になっていることがわかる。
論文 pp.7 Fiture 2より引用し自分なりのメモを追記
各ステップの概要については3.4に記述がある。あるいはこちらのGitHubのサンプル実装からも流れを追うことができる(むっちゃ読みづらい)。
量子アルゴリズムに全く無知な私の理解としては、エラーeはガウス分布から取ってきているので、それをガウスに関係する非線形変換とフーリエ関数を使ってなんとか逆変換してやろう、ということかと理解している。
考察 (3.7 Additional discussions)
上記のグラフを見ると、State 2の時点で分布が完全にランダムではないことがわかる。これを見て、まずState 2から直接LWE問題を解くことを試みたが、それは失敗に終わった。しかし、ここから、Step 3~5で係数を分割すればよいという気付きを得た。そうして、より小さな係数に取り組んだ結果、LWE問題を解くことに成功した。
個人的な感想
量子アルゴリズムのことはサッパリ分からないが、各ステップの組み合わせによってはより現実に近い設定を解く可能性もあると感じた。
PQCもどこまでいっても計算量的安全性に基づいているに過ぎないため、今後のこういった研究をもとに、適切なセキュリティパラメータが決められていくのだろうと思う。