🍚 blog

Publicly Auditable MPC for Private Voting Protocol

ENG
cryptography

Introduction

Collaboration across corporate boundaries is increasing every year. One hospital is working with another to build a versatile medical diagnostic AI. One factory is collaborating with another to build an AI that detects unauthorized access. However, user privacy is essential to such collaboration, and multi-party computation (MPC) is a promising technology that allows multiple parties to collaborate on computations while protecting the privacy of their data.

In situations where the results of data analysis calculations are publicly disclosed, such as voting or market analysis, it is necessary to enable anyone to verify the validity of the calculation results. Publicly Auditable MPC (PA-MPC) makes this possible.

This article provides an overview of PA-MPC and discusses its practice and future issues through the implementation of the Private Voting Protocol.

Publicly Auditable MPC (PA-MPC)

Publicly Auditable MPC (PA-MPC) is an MPC that public can verify the computation was performed correctly with respect to commitments to the inputs.

UseCase 1: Healthcare statistics

It calculates the cost of the health care system without revealing their history of visits to the hospital. The public will have an overall picture of the costs incurred by the health care system.

UseCase 2: Credit scores

Some agencies calculate a user's credit score without disclosing any transaction information they have with each other. The user can verify that the calculated credit score is correct.

Implementation

Collaborative zkSNARKs

Collaborative zk-SNARKs generates a proof about the secret value w = (w_1, w_2, ..., ... , w_N) distributed among multiple parties without revealing their witness to each other. The final proof size is constant.

Currently, it supports Groth16, Plonk and Marlin.

To run this, you clone this repo and run the command below then it runs a benchmark for calculating a^n.

cd mpc-snarks
cargo build --release --bin proof
./scripts/print.zsh groth16 spdz 10 2

That 10 means a and 2 means the number of party n.

As a result, you can see how much it spends for each step. You can see only the total time when running bench.zsh instead of print.zsh.

Start:   Connecting
··Start:   To king 1
··End:     To king 1 ...............................................................285.750µs
··Start:   From king 1
··End:     From king 1 .............................................................123.750µs
End:     Connecting ................................................................882.834µs
Start:   Groth16::Generator
··Start:   Constraint synthesis
··End:     Constraint synthesis ....................................................90.708µs
··Start:   Inlining LCs
··End:     Inlining LCs ............................................................78.833µs
··Start:   Constructing evaluation domain
··End:     Constructing evaluation domain ..........................................241.875µs
··Start:   R1CS to QAP Instance Map with Evaluation
····Start:   Evaluate Lagrange coefficients
····End:     Evaluate Lagrange coefficients ........................................19.500µs
··End:     R1CS to QAP Instance Map with Evaluation ................................155.250µs
··Start:   Compute G2 table
··End:     Compute G2 table ........................................................7.755ms
··Start:   Calculate B G2
··End:     Calculate B G2 ..........................................................2.932ms
··Start:   Compute G1 window table
··End:     Compute G1 window table .................................................2.802ms
··Start:   Generate the R1CS proving key
····Start:   Calculate A
····End:     Calculate A ...........................................................596.833µs
····Start:   Calculate B G1
····End:     Calculate B G1 ........................................................524.709µs
····Start:   Calculate H
····End:     Calculate H ...........................................................729.083µs
····Start:   Calculate L
····End:     Calculate L ...........................................................475.084µs
··End:     Generate the R1CS proving key ...........................................5.550ms
··Start:   Generate the R1CS verification key
··End:     Generate the R1CS verification key ......................................1.132ms
··Start:   Convert proving key elements to affine
··End:     Convert proving key elements to affine ..................................119.209µs
End:     Groth16::Generator ........................................................23.185ms
Start:   do the mpc (cheat)
··Start:   From king 32
··End:     From king 32 ............................................................85.792µs
··Start:   From king 32
··End:     From king 32 ............................................................68.167µs
··Start:   From king 32
··End:     From king 32 ............................................................76.333µs
··Start:   From king 32
··End:     From king 32 ............................................................98.875µs
··Start:   From king 32
··End:     From king 32 ............................................................69.041µs
··Start:   From king 32
··End:     From king 32 ............................................................68.583µs
··Start:   From king 32
··End:     From king 32 ............................................................66.542µs
··Start:   From king 32
··End:     From king 32 ............................................................61.292µs
··Start:   From king 32
··End:     From king 32 ............................................................76.125µs
··Start:   From king 32
··End:     From king 32 ............................................................45.750µs
··Start:   Broadcast 32
··End:     Broadcast 32 ............................................................430.916µs
··Start:   Broadcast 32
··End:     Broadcast 32 ............................................................327.208µs
··Start:   Broadcast 64
··End:     Broadcast 64 ............................................................141.958µs
End:     do the mpc (cheat) ........................................................1.982ms
Start:   timed section
··Start:   zk sampling
··End:     zk sampling .............................................................1.166µs
··Start:   Groth16::Prover
····Start:   Constraint synthesis
····End:     Constraint synthesis ..................................................10.084µs
····Start:   Inlining LCs
····End:     Inlining LCs ..........................................................22.083µs
····Start:   R1CS to QAP witness map
······Start:   batch product
········Start:   Broadcast 520
········End:     Broadcast 520 .....................................................283.791µs
········Start:   Broadcast 32
········End:     Broadcast 32 ......................................................384.291µs
········Start:   Broadcast 552
········End:     Broadcast 552 .....................................................256.750µs
········Start:   Broadcast 520
········End:     Broadcast 520 .....................................................198.000µs
········Start:   Broadcast 32
········End:     Broadcast 32 ......................................................300.125µs
········Start:   Broadcast 552
········End:     Broadcast 552 .....................................................221.334µs
······End:     batch product .......................................................1.831ms
····End:     R1CS to QAP witness map ...............................................1.947ms
····Start:   crypto
······Start:   Compute C
········Start:   MSM inner
··········Start:   Base MSM
··········End:     Base MSM ........................................................1.570ms
··········Start:   Base MSM
··········End:     Base MSM ........................................................1.532ms
········End:     MSM inner .........................................................3.143ms
········Start:   MSM inner
··········Start:   Base MSM
··········End:     Base MSM ........................................................1.236ms
··········Start:   Base MSM
··········End:     Base MSM ........................................................1.203ms
········End:     MSM inner .........................................................2.485ms
········Start:   SS scalar multiplication
··········Start:   Broadcast 48
··········End:     Broadcast 48 ....................................................259.833µs
··········Start:   Broadcast 32
··········End:     Broadcast 32 ....................................................316.792µs
··········Start:   Broadcast 80
··········End:     Broadcast 80 ....................................................243.958µs
··········Start:   Broadcast 32
··········End:     Broadcast 32 ....................................................285.750µs
··········Start:   Broadcast 32
··········End:     Broadcast 32 ....................................................258.667µs
··········Start:   Broadcast 64
··········End:     Broadcast 64 ....................................................173.709µs
········End:     SS scalar multiplication ..........................................3.803ms
······End:     Compute C ...........................................................9.947ms
······Start:   Compute A
········Start:   MSM size 11 11
··········Start:   MSM inner
············Start:   Base MSM
············End:     Base MSM ......................................................1.188ms
············Start:   Base MSM
············End:     Base MSM ......................................................1.172ms
··········End:     MSM inner .......................................................2.404ms
········End:     MSM size 11 11 ....................................................2.422ms
········Start:   SS scalar multiplication
··········Start:   Broadcast 48
··········End:     Broadcast 48 ....................................................281.208µs
··········Start:   Broadcast 32
··········End:     Broadcast 32 ....................................................333.334µs
··········Start:   Broadcast 80
··········End:     Broadcast 80 ....................................................285.750µs
··········Start:   Broadcast 32
··········End:     Broadcast 32 ....................................................296.000µs
··········Start:   Broadcast 32
··········End:     Broadcast 32 ....................................................204.333µs
··········Start:   Broadcast 64
··········End:     Broadcast 64 ....................................................205.500µs
········End:     SS scalar multiplication ..........................................3.717ms
······End:     Compute A ...........................................................6.576ms
······Start:   Compute B in G1
········Start:   MSM size 11 11
··········Start:   MSM inner
············Start:   Base MSM
············End:     Base MSM ......................................................999.333µs
············Start:   Base MSM
············End:     Base MSM ......................................................986.375µs
··········End:     MSM inner .......................................................2.026ms
········End:     MSM size 11 11 ....................................................2.033ms
······End:     Compute B in G1 .....................................................2.402ms
······Start:   Compute B in G2
········Start:   MSM size 11 11
··········Start:   MSM inner
············Start:   Base MSM
············End:     Base MSM ......................................................3.218ms
············Start:   Base MSM
············End:     Base MSM ......................................................3.118ms
··········End:     MSM inner .......................................................6.372ms
········End:     MSM size 11 11 ....................................................6.379ms
········Start:   SS scalar multiplication
··········Start:   Broadcast 48
··········End:     Broadcast 48 ....................................................267.666µs
··········Start:   Broadcast 32
··········End:     Broadcast 32 ....................................................364.166µs
··········Start:   Broadcast 80
··········End:     Broadcast 80 ....................................................204.916µs
··········Start:   Broadcast 32
··········End:     Broadcast 32 ....................................................247.833µs
··········Start:   Broadcast 32
··········End:     Broadcast 32 ....................................................251.334µs
··········Start:   Broadcast 64
··········End:     Broadcast 64 ....................................................252.375µs
········End:     SS scalar multiplication ..........................................3.186ms
······End:     Compute B in G2 .....................................................10.873ms
······Start:   Finish C
······End:     Finish C ............................................................5.208µs
····End:     crypto ................................................................29.839ms
··End:     Groth16::Prover .........................................................31.874ms
··Start:   reveal
····Start:   Broadcast 48
····End:     Broadcast 48 ..........................................................176.208µs
····Start:   Broadcast 32
····End:     Broadcast 32 ..........................................................212.209µs
····Start:   Broadcast 80
····End:     Broadcast 80 ..........................................................129.250µs
····Start:   Broadcast 96
····End:     Broadcast 96 ..........................................................357.750µs
····Start:   Broadcast 32
····End:     Broadcast 32 ..........................................................245.167µs
····Start:   Broadcast 128
····End:     Broadcast 128 .........................................................225.750µs
····Start:   Broadcast 48
····End:     Broadcast 48 ..........................................................223.625µs
····Start:   Broadcast 32
····End:     Broadcast 32 ..........................................................290.125µs
····Start:   Broadcast 80
····End:     Broadcast 80 ..........................................................234.750µs
··End:     reveal ..................................................................9.525ms
End:     timed section .............................................................41.478ms
Stats: Stats {
    bytes_sent: 10944,
    bytes_recv: 10944,
    broadcasts: 33,
    to_king: 0,
    from_king: 0,
}

I show the result of running the scripts above using my Mac Studio (Apple M2 Max, 64GB Memory, 1TB Storage). In this benchmark, SPDZ executes MPC with local processes, without LAN/WAN. Thus, network latency is super low.

SPDZ takes 2~2.5 times more than on local (non MPC).

n=2 3 4
plonk(spdz) 201.101ms 224.254ms 229.906ms
plonk(local) 88.303ms - -
groth16(spdz) 29.428ms 31.035ms 35.302ms
groth16(local) 9.619ms - -
marlin(spdz) 62.336ms 68.510ms 79.011ms
marlin(local) 39.053ms - -

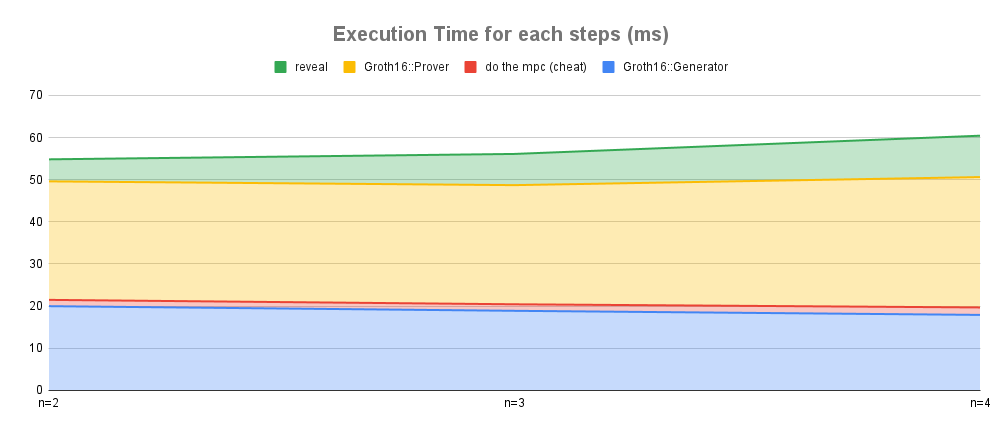
The graph shows execution time transition for each steps. The circuit generation time and proof generation time occupy more than 80% of whole time. And the proof generation and revealing time increased with n.

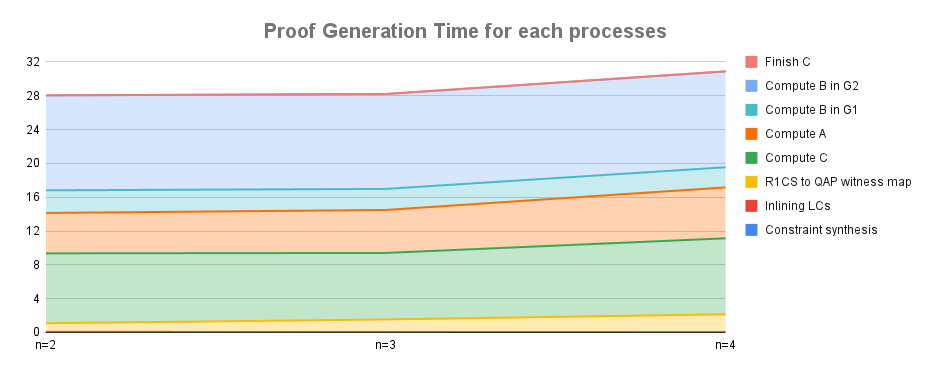
Next graph shows proof generation time separated by processes. Computing B in G2 and Computing C use more time like 8~11ms. Comparing to n=4 with n=2, R1CS to QAP witness map takes almost twice time, and Compute C, Compute A, Compute B in G2 take 0.5~1.3ms more.

A closer look revealed that the execution time of SS scalar multiplication, which performs broadcasts, increased. Conversely, MSM, which does not perform broadcasts, remained constant even as n increased.

Next, let’s see about the programs.

mpc-snarks/src/proof.rs runs firstly when you run the script.

After that, mpc() of mod Plonk is called. In this function, instantiates the circuit, generates proof and verify it.

            fn mpc<E: PairingEngine, S: PairingShare<E>>(n: usize, timer_label: &str) {
                let rng = &mut test_rng();
                let circ_no_data = plonk_squaring_circuit(RepeatedSquaringCircuit::without_data(n));
                let circ_no_data = CircuitLayout::from_circuit(&circ_no_data);

                let a = E::Fr::rand(rng);
                let circ_data = mpc_squaring_circuit::<
                    E::Fr,
                    <MpcPairingEngine<E, S> as PairingEngine>::Fr,
                >(a, n);
                let plonk_circ_data = plonk_squaring_circuit(circ_data.clone());
                let plonk_circ_data = CircuitLayout::from_circuit(&plonk_circ_data);
                let public_inputs = std::iter::once((
                    "out".to_owned(),
                    circ_data.chain.last().unwrap().unwrap().reveal(),
                ))
                .collect();
                let setup_rng = &mut test_rng();
                let zk_rng = &mut test_rng();
                let srs =
                    MarlinPcPlonk::<E::Fr, E>::universal_setup(n.next_power_of_two(), setup_rng);
                let (pk, vk) = MarlinPcPlonk::<E::Fr, E>::circuit_setup(&srs, &circ_no_data);
                let mpc_pk = Reveal::from_public(pk);
                MpcMultiNet::reset_stats();
                let t = start_timer!(|| timer_label);
                let pf = channel::without_cheating(|| {
                    let pf = MarlinPcPlonk::<
                        <MpcPairingEngine<E, S> as PairingEngine>::Fr,
                        MpcPairingEngine<E, S>,
                    >::prove(&mpc_pk, &plonk_circ_data, zk_rng);

                    let reveal_timer = start_timer!(|| "reveal");
                    let pf = pf.reveal();
                    end_timer!(reveal_timer);
                    pf
                });
                end_timer!(t);
                MarlinPcPlonk::<E::Fr, E>::verify(&vk, &circ_no_data, pf, &public_inputs);
            }

In mpc_squaring_circuit(), each party generates the share of a, then builds the circuit for Collaborative zkSNARKs.

    fn mpc_squaring_circuit<Fr: Field, MFr: Field + Reveal<Base = Fr>>(
        start: Fr,
        squarings: usize,
    ) -> RepeatedSquaringCircuit<MFr> {
        let raw_chain: Vec<Fr> = std::iter::successors(Some(start), |a| Some(a.square()))
            .take(squarings + 1)
            .collect();
        let rng = &mut test_rng();
        let chain_shares = MFr::king_share_batch(raw_chain, rng);
        RepeatedSquaringCircuit {
            chain: chain_shares.into_iter().map(Some).collect(),
        }
    }

Current Limitations:

  • Circuit’s Flexibility is as same as basic zkSNARKs.
  • Programs like accessing to shared data and branching based on them are not supported.
  • RAM machine Execution is not covered.
  • It supports at most n=4.
  • follows SPDZ’s security model
    • threshold corruption: a constant number of parties are thought to be corrupted
    • malicious-with-abort model: honest players will abort the protocol when the adversary deviates from the protocol

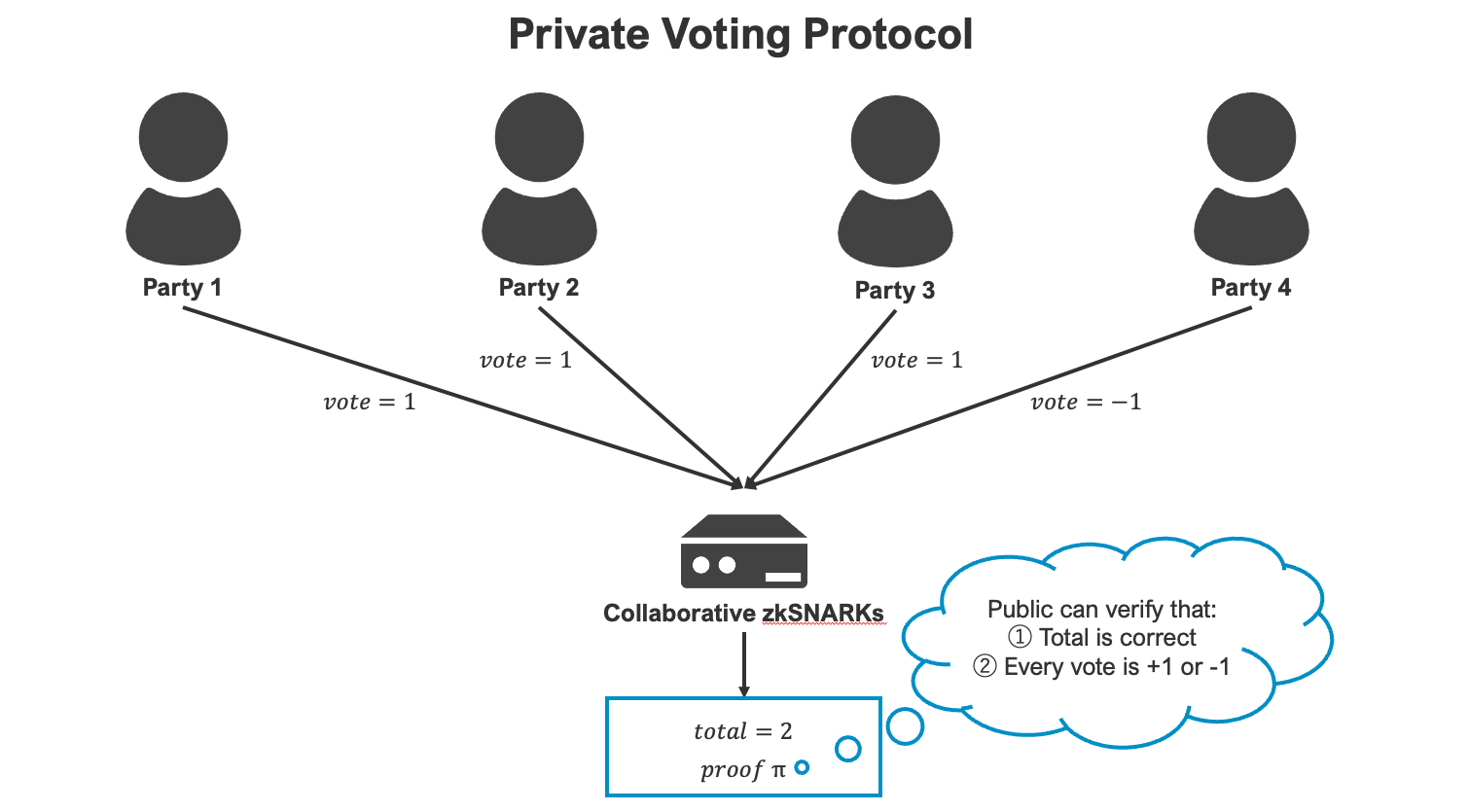
Private Voting Protocol using Collaborative zkSNARKs

Next, I modify some code to implement the Private Voting Protocol which calculates the sum of each party’s vote {1, -1}. The final impl’s PR is here.

link_preview

First, I implement struct VotingCircuit. I should also implement that trait.

    #[derive(Clone)]
    struct VotingCircuit<F: Field> {
        inputs: Vec<Option<F>>,
        total: Option<F>,
    }

Next, I implement mpc_voting_circuit(). Here, each party party receives their votes as shares, and calculates the sum with MPC.

    fn mpc_voting_circuit<Fr: Field, MFr: Field + Reveal<Base = Fr>>(
        votes: usize,
    ) -> VotingCircuit<MFr> {
        let rng = &mut test_rng();
        let shared_inputs: Vec<MFr> = (0..votes).map(|_| {
            if rand::random::<bool>() {
                MFr::king_share(Fr::one(), rng)
            } else {
                MFr::king_share(-Fr::one(), rng)
            }
        }).collect();
        let shared_total = shared_inputs.iter()
            .fold(MFr::zero(), |acc, &input| acc + input);

        VotingCircuit {
            inputs: shared_inputs.into_iter().map(Some).collect(),
            total: Some(shared_total),
        }
    }

Next, I implement zkCircuit. We have two constraints.

  • checking if input is +1 or -1.
  • checking if the sum is correct.
    impl<ConstraintF: Field> ConstraintSynthesizer<ConstraintF>
        for VotingCircuit<ConstraintF>
    {
        fn generate_constraints(
            self,
            cs: ConstraintSystemRef<ConstraintF>,
        ) -> Result<(), SynthesisError> {
            let mut sum_lc = LinearCombination::<ConstraintF>::zero();
            for input_opt in self.inputs.iter() {
                let input_var = cs.new_witness_variable(|| input_opt.ok_or(SynthesisError::AssignmentMissing))?;

                // input * input should be 1 (input should be +1 or -1)
                cs.enforce_constraint(
                    lc!() + input_var,
                    lc!() + input_var,
                    lc!() + Variable::One,
                )?;

                sum_lc = sum_lc + (ConstraintF::one(), input_var);
            }

            let total_var = cs.new_input_variable(|| self.total.ok_or(SynthesisError::AssignmentMissing))?;
            cs.enforce_constraint(
                sum_lc,
                lc!() + Variable::One,
                lc!() + total_var,
            )?;

            Ok(())
        }
    }

Finally, I change something to run those functions. Please watch my PR for more details (I only implements for groth16).

After those changes, run the script again and you obtain these results below.

cargo build --release --bin proof
RUST_BACKTRACE=1 ./scripts/print.zsh groth16 spdz 10 4
> ...
> total is 4

And, if you change the share as 2, the verification should fail.

> Verify result: false

As performance, the execution time is almost same as sample implementation.

The circuit complexity is not so different from sample.

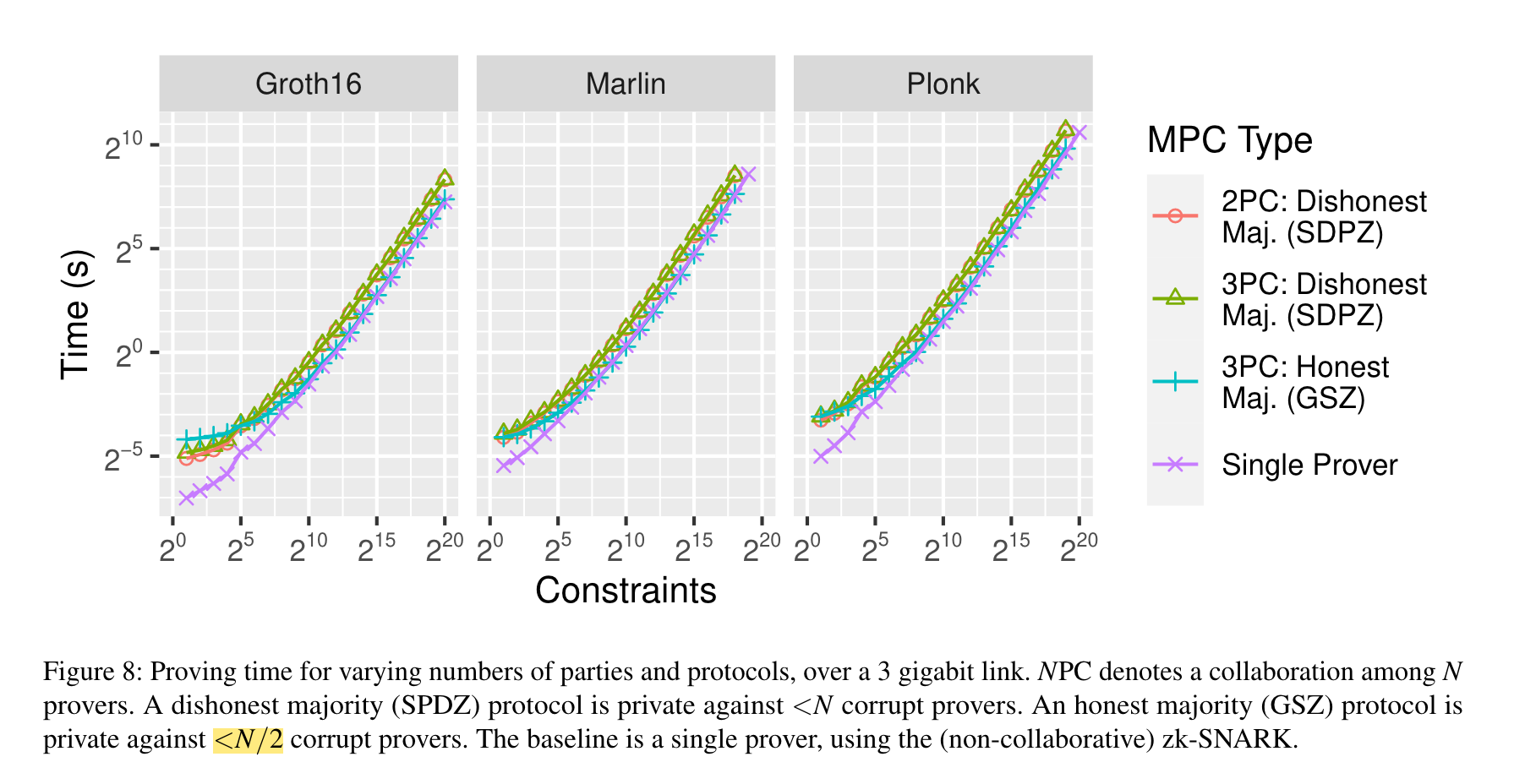
According to the paper, execution time increases linearly with the number of constraints.

https://www.usenix.org/conference/usenixsecurity22/presentation/ozdemir

Discussion

In the future, it should be possible to support DNA sequence alignment and other. Currently, however, it is difficult to support some complex computations, like branching program based on the shared data (c.f. Database). First we discuss the hurdles.

zkSNARKs basically supports circuit evaluation, not RAM machine execution. However, Rust programming language targets RAM machine execution. Stacked Garbling directly supports branching programs.

Next, we consider about combining Garbled Circuit with zkSNARKs as alternative approach against Collaborative zkSNARKs. However, Garbled Circuit requires all gates to be encrypted using a symmetric key cryptography such as AES, which is incompatible with zkSNARKs because this cryptography is not an arithmetic operation. In other words, the execution of the Garbled Circuit, made more efficient by AES, will likely be made inefficient by zkSNARKs.

Thus, this problem may be alleviated by using techniques such as Lookup Table. However, research is still in progress, as it requires more complex configurations. zk-Fabric combines Garbled Circuit and zk Circuit using partitioned garbled circuits.

Conclusion

This article described the PA-MPC technology through the implementation of the Private Voting Protocol using Collaborative zkSNARKs and discussed the challenges and possibilities in this area.

Reference

← Go home