Introduction

Netting, the process through which companies offset mutual debts while conducting transactions, plays a critical role in conserving liquidity and reducing settlement costs [7]. To execute netting, companies must disclose invoices to a central authority, such as the government. However, this requirement poses a significant barrier. In Slovenia, only 1.2% of companies have participated in the network due to this challenge [8]. To address this issue, there is a growing demand for Private Netting processes that enable the execution of netting while keeping invoice details confidential.

The Netting process can be mapped to the Minimum Cost Flow Problem, a type of mathematical optimization, as proposed by Fleischman et al. [7]. Therefore, this paper focuses on the Network Simplex Method, a well-known algorithm for this problem, and proposes an MPC-based (Multi-Party Computation) algorithm to ensure privacy in the netting process.

Network Simplex

The Network Simplex Method is a technique for solving the minimum cost flow problem by repeatedly swapping edges of an initial solution. The overall algorithm becomes more efficient by efficiently searching for the edges to be swapped. Benchmarking by Goldberg [1] has reported it to be the most efficient among MCF algorithms. It is also implemented in the minimum_cost_flow function of NetworkX [2]. However, the algorithm is not simple. The following example will explain the algorithm step-by-step, based on Orlin's polynomial-time algorithm [3] and Brunovsky's blog [4].

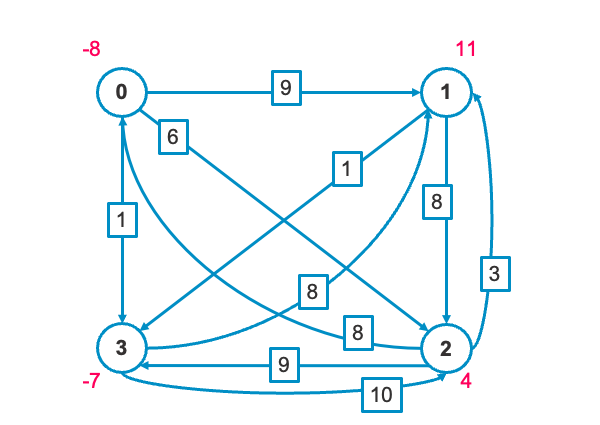
0. Sample Obligation Network

To explain using a sample, let's consider the following graph. It consists of four nodes labeled 0, 1, 2, and 3. The numbers on the edges indicate the original flow. The red numbers on the nodes represent the demand.

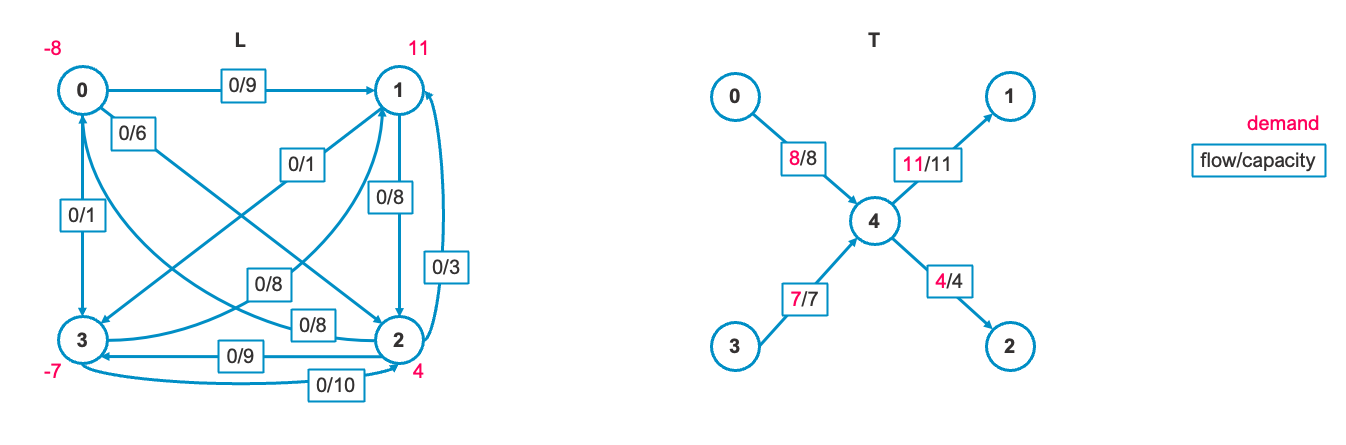
1. Create Artificial Graph and make Initial Feasible Flow

First, define the original graph's flow as the capacity and set the flow to zero to create graph L. This is where the algorithm starts.

To obtain the initial feasible solution, we create an artificial graph T. Here, we define a dummy node 4 and add edges from each supply node to node 4 and from node 4 to each demand node, with flow and capacity equal to their respective supply and demand.

Each edge in this graph satisfies the optimality conditions. Here's how the graph (L,T) looks:

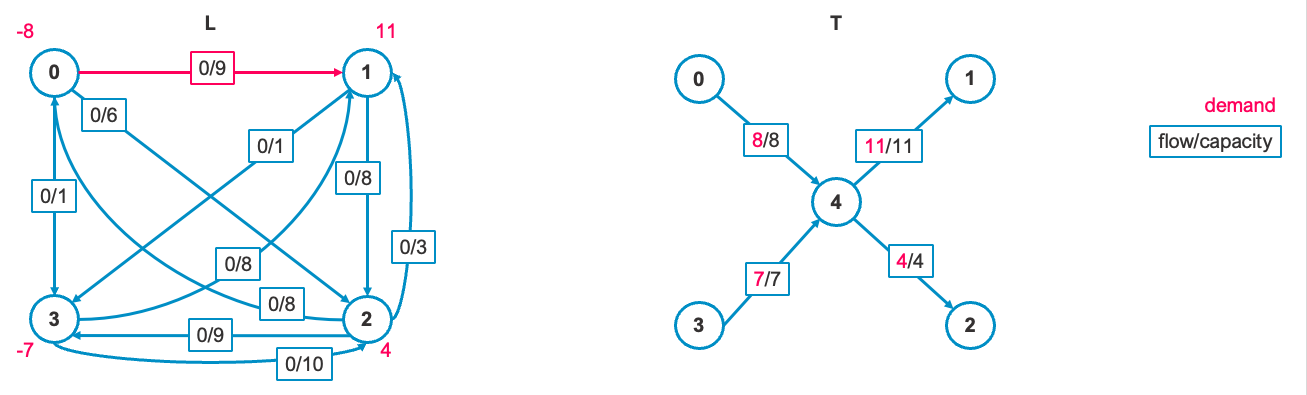
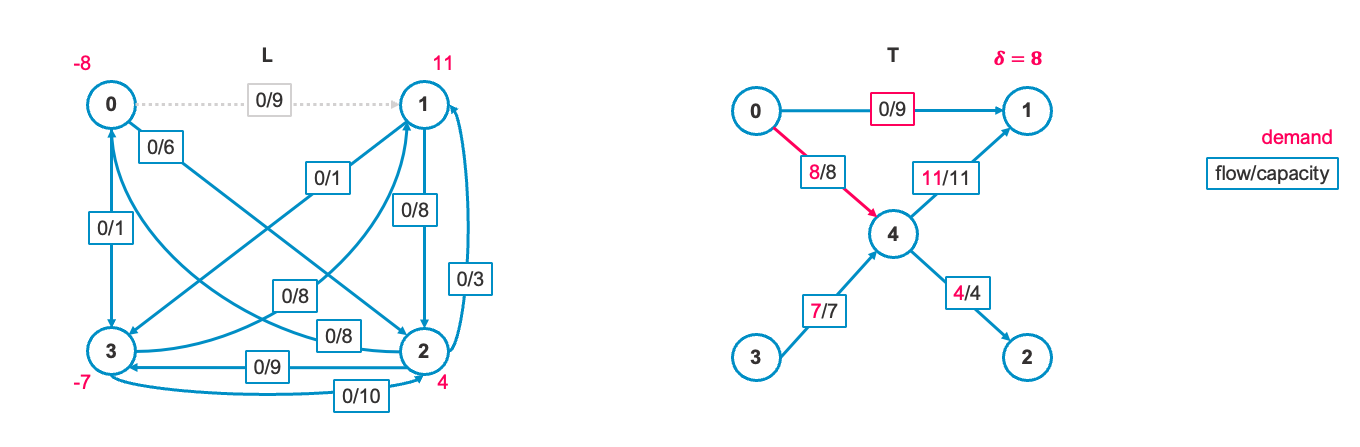
2. Find entering edge e_in

Next, we need to find the entering edge e_{in} from the set L. The e_{in} refers to the edge that extends from a supply node to a demand node. Orlin's algorithm defines another variable called "potential" to search for this edge. Now, edge (0,1) is selected as e_{in}.

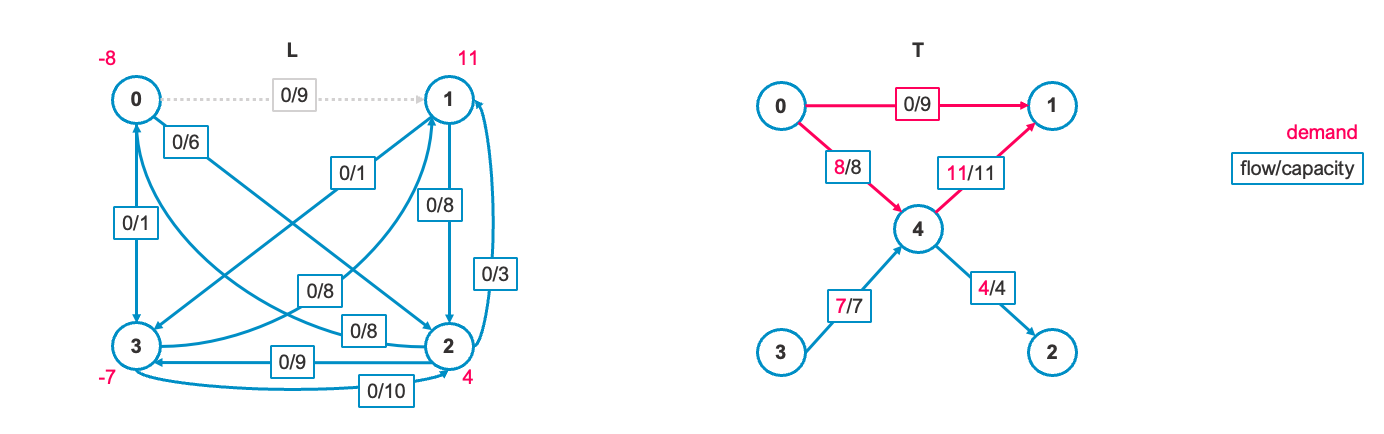
3. Pivot

3-1. Find cycle including T+\{e_{in}\}

We add the entering edge e_{in} to T and identify a cycle within T. Then we will look for a cycle in the graph, ignoring the edge directions. The cycle is 0 \rightarrow 1 \rightarrow 4 \rightarrow 0.

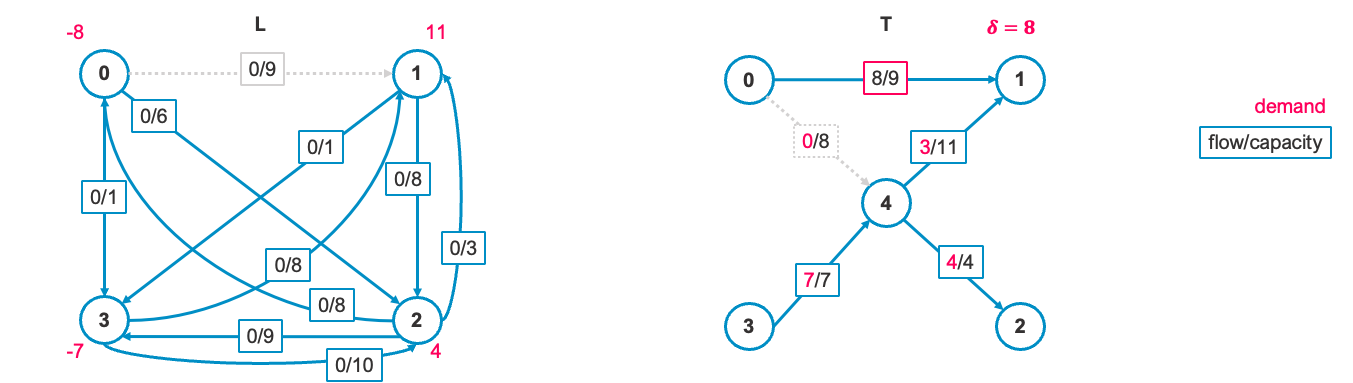
3-2. Detect leaving edge e_out and update flow

We define the minimum flow \delta in the cycle and identify the leaving edge e_{out}, which is the edge with the minimum flow value in the cycle. The minimum flow \delta = 8 here, and e_{out} = (0,4).

We update the flow in the cycle by adding \delta to the entering edge e_{in} and subtracting \delta from the other edges in the cycle. Since e_{out} becoms zero-flow, it is moved from T to L.

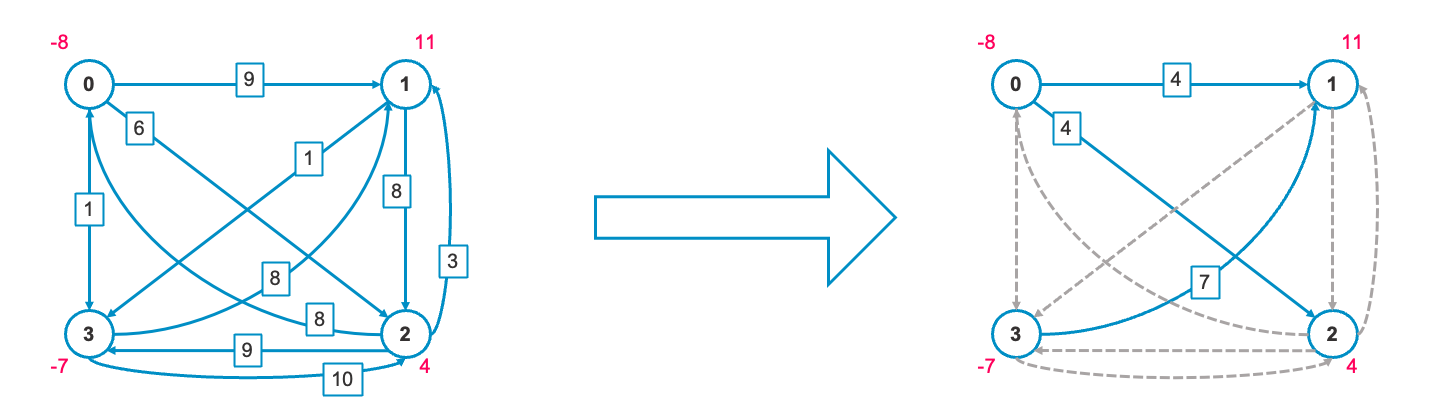
With the pivot operation completed, we now return to finding the next entering edge. If no entering edge is found, the algorithm terminates. The final optimal solution looks:

Finally, The total time complexity of this algorithm is O(\min(|V|\cdot|E|\cdot log|V|C, |V|\cdot|E|^2\cdot log|V|). The bulk of the algorithm's complexity hinges on the efficiency of finding the entering edge.

Performance Analysis

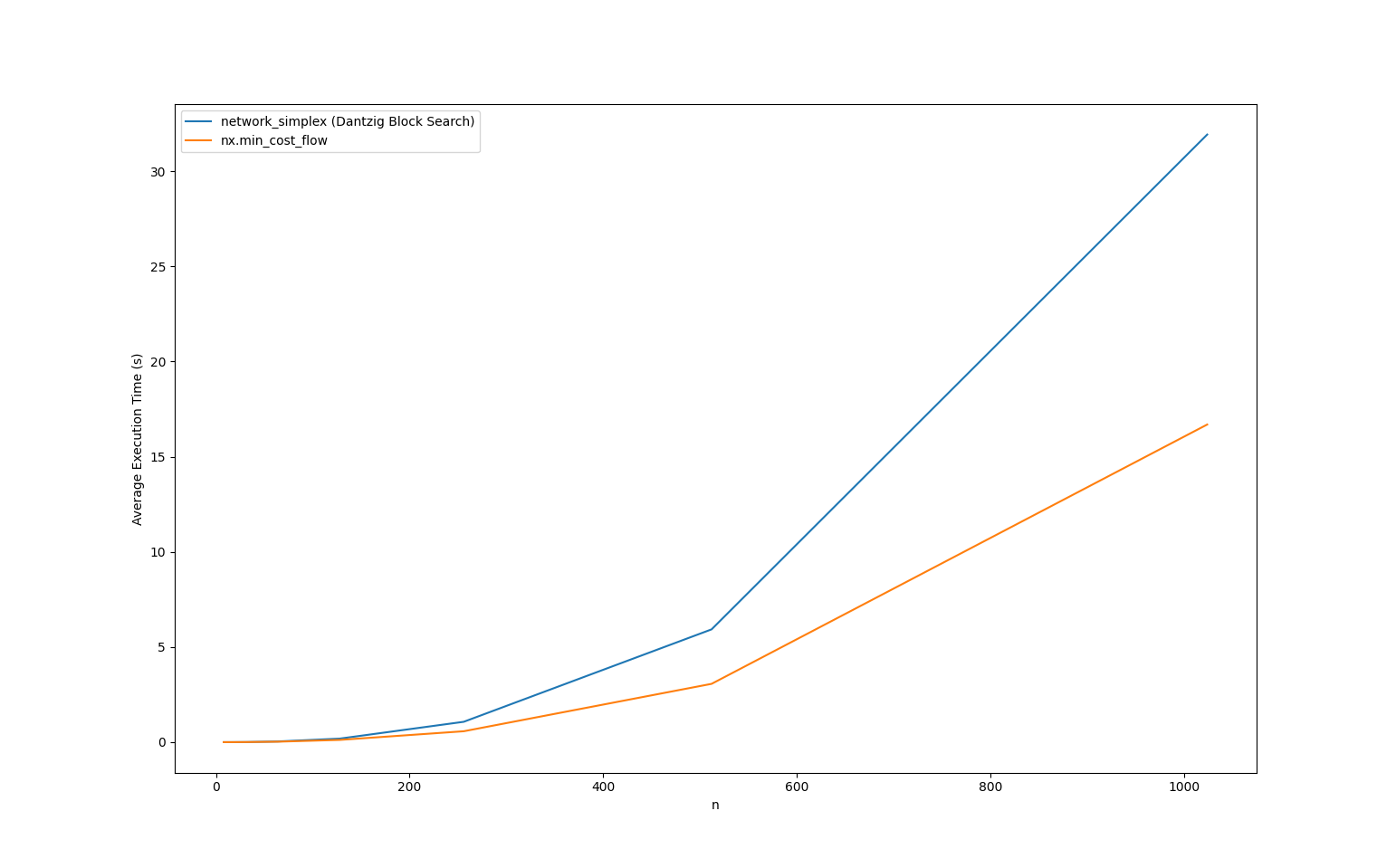
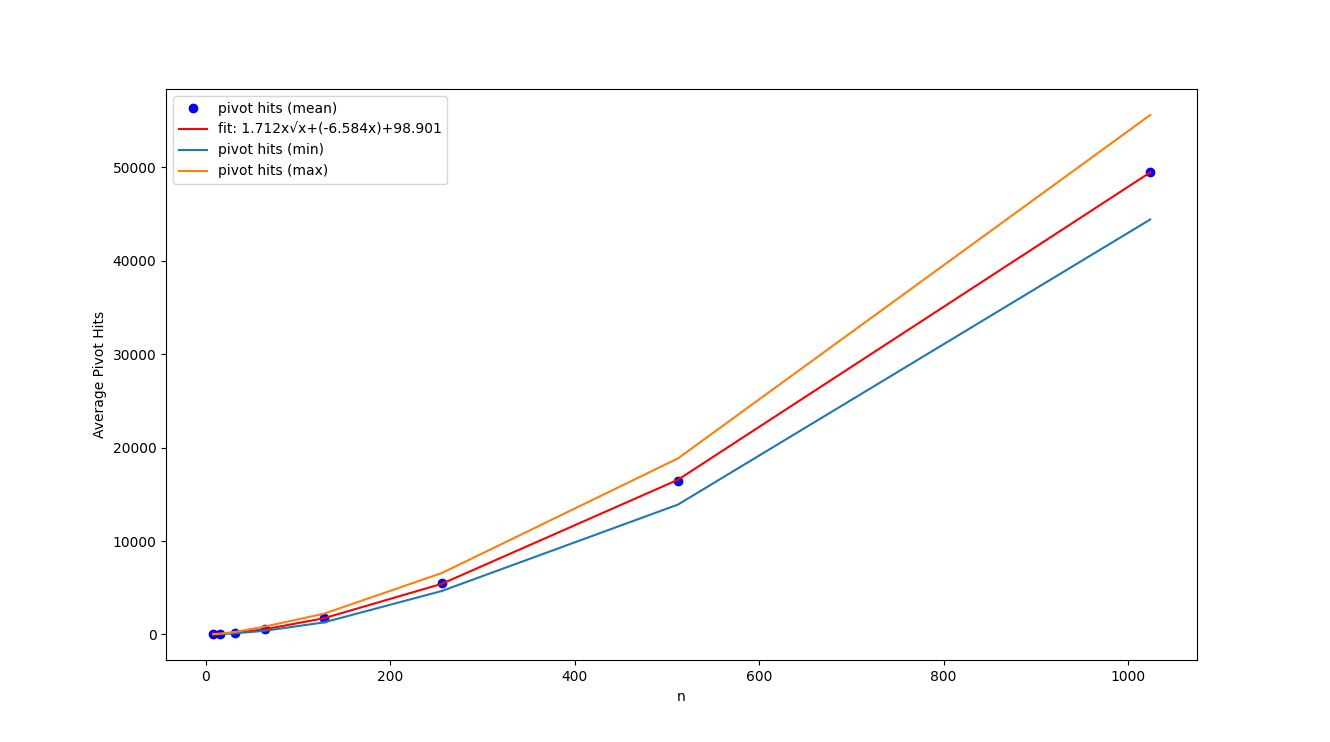
Here are the benchmark results comparing our implementation with the NetworkX implementation. We varied the number of vertices V while keeping E = V^2 and \ c_{ij}=1 \ \ \forall{(i,j)} fixed.

The results show that the optimal solution is obtained in approximately 15~30 seconds when V=2^{10}. The time complexity increases quadratically as Vincreases.

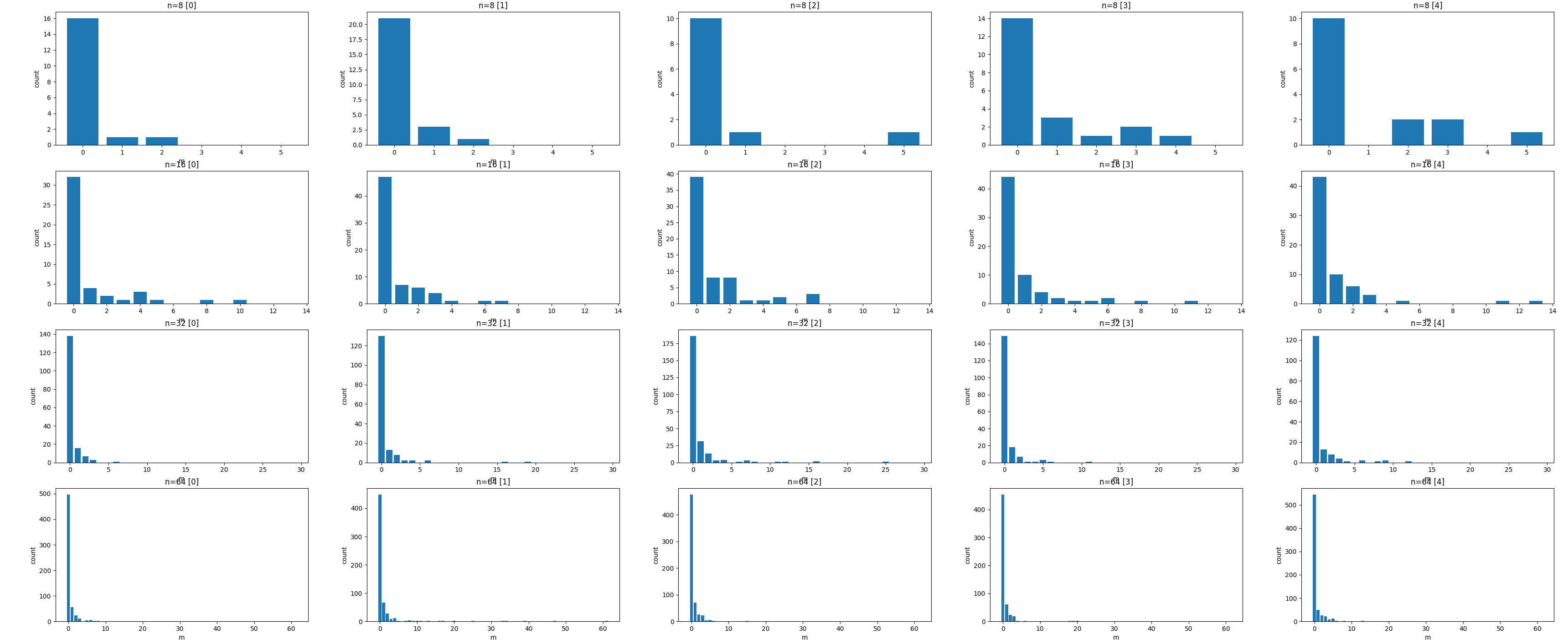
Next, we evaluate the computational complexity. By plotting the number of pivots required for each value of V, we found that the results can be approximated by O(V\sqrt{V}).

Furthermore, when executing the "find entering edge" operation using block search, we observed that the most frequent discovery of the entering edge occurred during the first search when the block size was set to \sqrt{E}.

Exactly. Given the observations from the block search method, the time complexity for finding the entering edge can be averaged to O(\sqrt E).

Histogram of the number of loops it took to find the entering edge, called m. The x-axis is m and the y-axis is the frequency of m. Each row is plotted 5 times at random, with each row varying the number of times it took to find the edge. Note that the edges are fixed atV^2.

Next, it is observed that the pivot operation itself can be executed in O(V) time.

Therefore, the overall time complexity of this algorithm is, on average, O(V\sqrt{V} \sqrt{E})=O(V^2\sqrt{V}).

In the worst-case scenario, the block search may proceed through \sqrt{E} blocks, each taking \sqrt{E} time, thus the time complexity of the Network Simplex Algorithm is O(V^3\sqrt{V}) in such case.

A note on implementing Secure Network Simplex

When implementing the Network Simplex algorithm using MPC (Multi-Party Computation), there are two primary concerns. These are based on our previous experience implementing Secure MMC [5].

1. Minimum Value Calculation

In Network Simplex, it's essential to calculate the minimum negative reduced cost on edges and the minimum residual flow in cycles. According to our benchmarks, these comparisons constitute 80% of the overall computational effort of the algorithm.

Toft [6] proposed a binary tree-based min algorithm that can compute the minimum value in O(log(n)), which could significantly optimize these calculations under MPC.

The sorting algorithm can also be applied to the calculation of the minimum value. Hamada [9] et. al. proposed efficient secure quick sort, which takes 1.410 seconds for sorting 1k items. Asharov et. al. [10] proposed efficient secure radix sort, which takes 2.261 seconds for sorting 1M items. In quick sort, we determines a certain threshold value and divides the values into sets greater than and less than the threshold value. In MPC, the threshold cannot be set to a median value, so a random value must be set. In Network Simplex, the median is often near 0, so a quick sort with 0 as the threshold would work efficiently. ,.

2. Optimality Check

After executing a pivot in Network Simplex, it's crucial to check if the current flow represents an optimal solution. If it is optimal, the algorithm should terminate. Repeating these checks for the worst-case scenario could equate the computational complexity to that of other algorithms. Under secure computation, performing these checks without revealing the values necessitates a pre-determined number of executions. This way, the result can be returned as an approximate optimal solution after a specific number of iterations.

Similarly, when finding the entering edge, it's essential to check if the calculated minimum reduced cost is negative. If it is negative, the loop should stop, and the algorithm should immediately proceed to the pivot operation.

Fortunately, benchmarks have provided an average number of iterations required for termination. The entire loop takes O(V\sqrt{V}) iterations, and finding the entering edge involves one search over \sqrt{E} blocks. By using these as pre-determined values, we can design the algorithm to terminate after these iterations and return the result as an approximate solution.

See more about secure network simplex here: http://link.springer.com/10.1007/978-3-642-03549-4_6

Reference

1. Andrew V Goldberg, “An Efficient Implementation of a Scaling Minimum-Cost Flow Algorithm”, Journal of Algorithms, Volume 22, Issue 1, 1997, Pages 1-29, ISSN 0196-6774, https://doi.org/10.1006/jagm.1995.0805.
2. network_simplex function of NetworkX, https://networkx.org/documentation/stable/_modules/networkx/algorithms/flow/networksimplex.html#network_simplex
3. Orlin, J.B. A polynomial time primal network simplex algorithm for minimum cost flows. Mathematical Programming 78, 109–129 (1997). https://doi.org/10.1007/BF02614365
4. Network Simplex by brunovsky blog, https://codeforces.com/blog/entry/94190
5. Enciro Bottazzi, Masato Tsutsumi, Nam Ngo, “A Note on Securely Finding Minimum Mean Cycle”, 2024, available on:https://ethresear.ch/t/a-note-on-securely-finding-minimum-mean-cycle/20073
6. Toft, T. (2009). Solving Linear Programs Using Multiparty Computation. In: Dingledine, R., Golle, P. (eds) Financial Cryptography and Data Security. FC 2009. Lecture Notes in Computer Science, vol 5628. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-03549-4_6
7. Fleischman, T.; Dini, P. Mathematical Foundations for Balancing the Payment System in the Trade Credit Market. J. Risk Financial Manag. 2021, 14, 452. https://doi.org/10.3390/jrfm14090452
8. Fleischman, T.; Dini, P.; Littera, G. Liquidity-Saving through Obligation-Clearing and Mutual Credit: An Effective Monetary Innovation for SMEs in Times of Crisis. J. Risk Financial Manag. 2020, 13, 295. https://doi.org/10.3390/jrfm13120295
9. Hamada, K., Kikuchi, R., Ikarashi, D., Chida, K., Takahashi, K. (2013). Practically Efficient Multi-party Sorting Protocols from Comparison Sort Algorithms. In: Kwon, T., Lee, MK., Kwon, D. (eds) Information Security and Cryptology – ICISC 2012. ICISC 2012. Lecture Notes in Computer Science, vol 7839. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-37682-5_15
10. Gilad Asharov, Koki Hamada, Dai Ikarashi, Ryo Kikuchi, Ariel Nof, Benny Pinkas, Katsumi Takahashi, and Junichi Tomida. 2022. Efficient Secure Three-Party Sorting with Applications to Data Analysis and Heavy Hitters. In Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security (CCS '22). Association for Computing Machinery, New York, NY, USA, 125–138. https://doi.org/10.1145/3548606.3560691