1. Introduction
Concept and History of FHE
Fully Homomorphic Encryption (FHE) enables computation of arbitrary functions over encrypted data.
This is, given encryptions
FHE history has started in 1978, within a year of publishing of the RSA scheme. The problem of constructing a FHE scheme was first published by Rivest, Adlemen and Dertouzos.
Gentry has developed first FHE scheme based on Lattice-based Cryptography in 2009, then published a simpler version allowing FHE over the integers, and finally developed the first scheme with bootstrapping (mention later).
In 2011, Brakerski, Gentry, Vaikuntanathan (BGW) developed an FHE scheme based on the Ring Learning With Errors (RLWE) problem. Then, Brakerski/Fan-Vercauteren (BFV) scheme was developed in 2012. On these schemes, the increase of noise is slower, and Leveled FHE mode is efficient enough for many applications even without invoking bootstrapping.
In 2013, Gentry, Sahai, Waters (GSW) proposed a technique for building FHE schemes that avoids an expensive “relinearization” step in homomorphic multiplication. Later, FHEW(2014) and TFHE(2016) schemes were developed based on GSW.
Goal of this article
This article aims to raise your resolution to the FHE technology and discusses how practical FHE can be, along with some practical examples and practices in implementation.
2. Basic Principles of FHE
FHE: Technical Principle
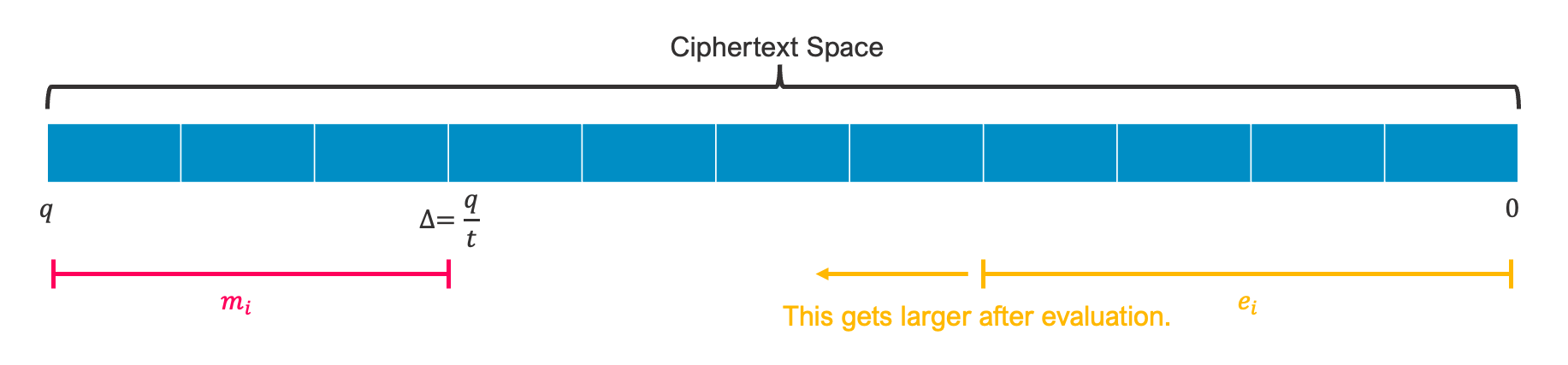
In Lattice-based Cryptography, which is the basis of FHE, represents all data such as SecretKey, Message, Ciphertext. And, when you want to encrypt the message
Then, the relationship between ciphertext modulo
fig2-1. Relationship between ciphertext space and each component
This figure means that
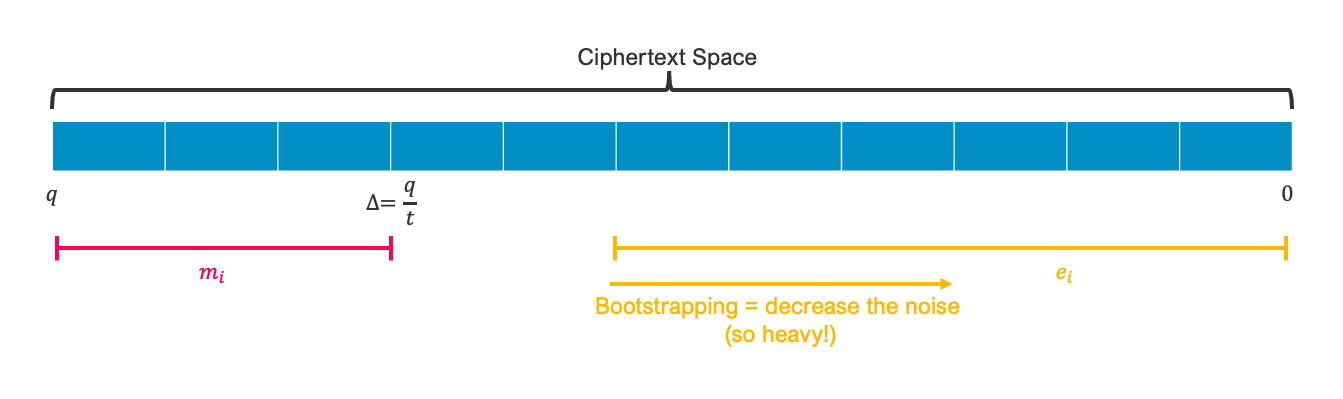
Bootstrapping
The technique “Bootstrapping” decreases that noise at some intervals. This needs to be used before the noise gets too large.
fig 2-2. Bootstrapping
FHE Protocol
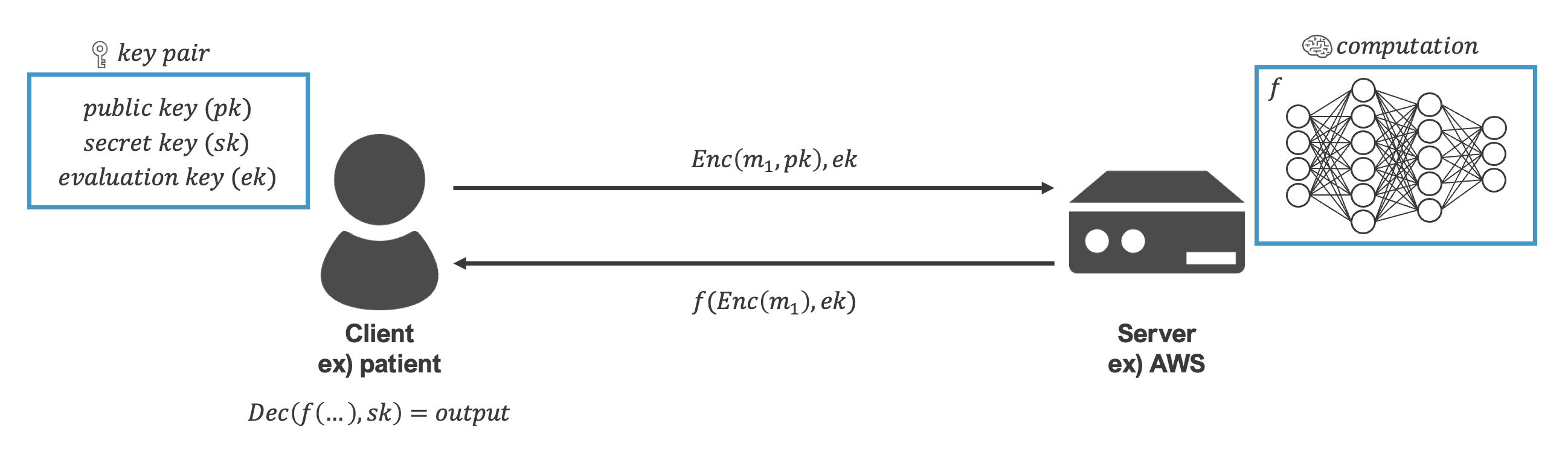
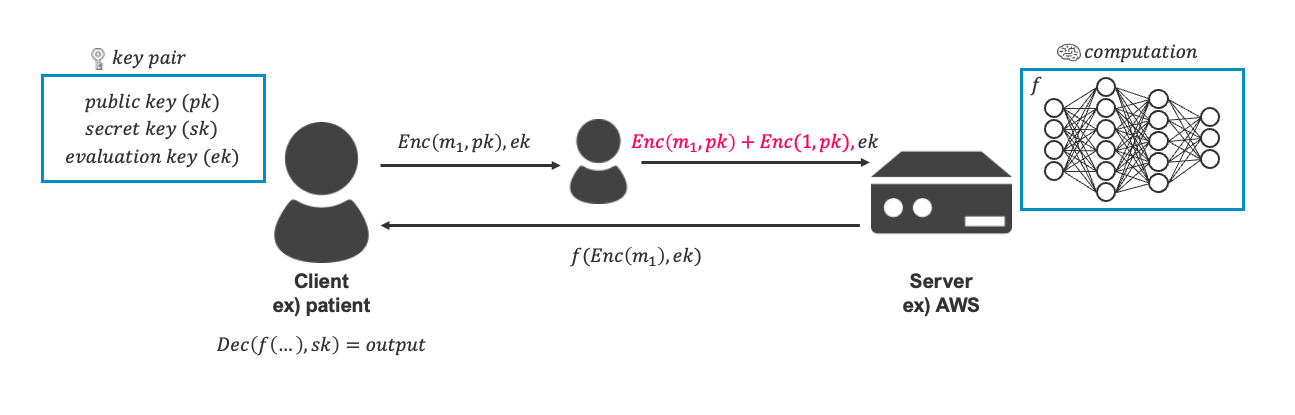
Next, FHE Process is shown in the following figure. At First, user (client) generates a key pair and encrypts data locally.
Then user sends the cipher-text and evaluation key ek to server.
Next, the server executes the function (ex: arithmetic operation, boolean operation) over encrypted data. ML inference is drawn as an example on the figure.
Finally, user decrypts the output after receiving it from server then user gains the result.
The data keeps encrypted while interaction between user and server.
fig2-3. FHE Step Overview
For more mathematic principle, refer to these resources:
- https://eprint.iacr.org/2021/204
- https://github.com/Janmajayamall/tfhe-research/blob/main/notes/TFHE.md
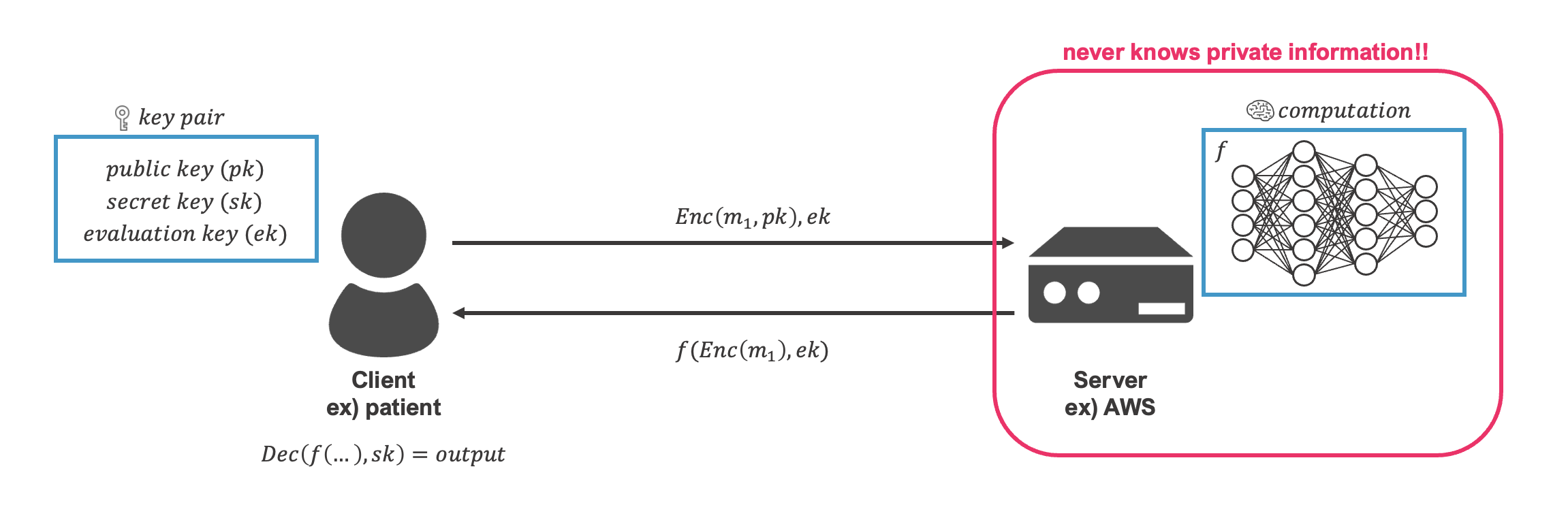
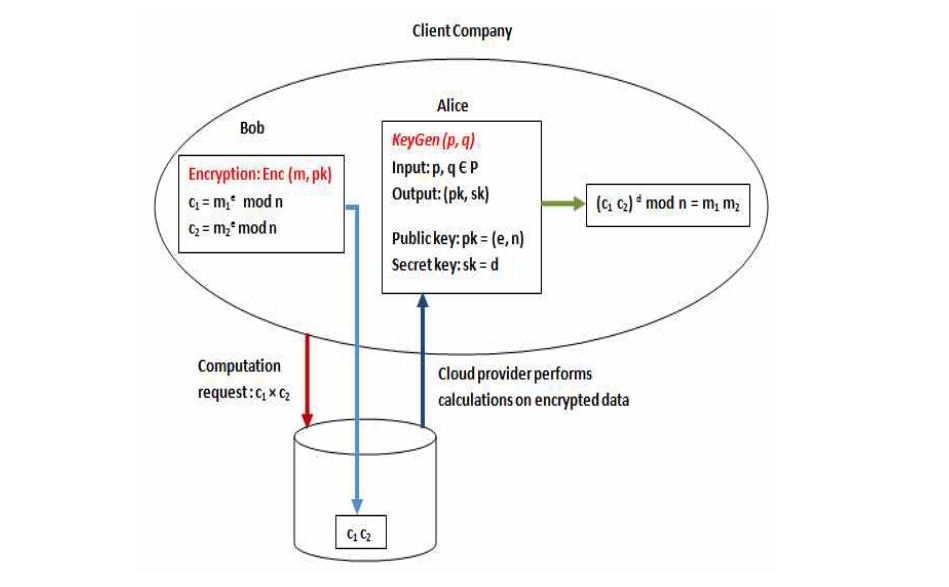
What FHE solves
Thus, this allows for data processing and analysis using cloud computing resources and other resources without sacrificing security, even when handling airtight information.
fig2-4. Server-side View of FHE
What FHE doesn’t solve
FHE, by design, never satisfies the security property “Non-malleability”. That is, an adversary can re-encrypt by adding/multiplying some values over a cipher-text. You need to combine other privacy-preserving technologies like ID-based Encryption, Verifiable Computation, and so on if you want to satisfy this.
fig2-5. An example that middleman adds some value over encrypted input
3. Technical Challenges and Updates
Challenges
- Bootstrapping Cost Overhead
As we show Bootstrapping above, this technique needs large computation. - Computing Complex Function
The complex function (sin, exp, …) is still difficult to compute because FHE basically applies on polynomial functions. If you replace complex function to approximately polynomial function, the accuracy will go down.
Computational Cost and Performance
I supplement the result for ML Inference using Concrete ML library in the following table.
| Model | Rounding | Test Data | Inference Time | Accuracy | |
|---|---|---|---|---|---|
| CIFAR10 Classification | 27Layer CNN | 5bits | 33232 colored image | 58.11sec / image | 89.21% |
| (-0.01%) | |||||
| MNIST Classification | 4Layer CNN | 6bits | 8*8 grayscale image | 10sec / image | 98.22% |
| (+0.00%) |
Execution Environment: Mac Studio Apple M2 Max 64GB Memory macOS 14.0
Or you can see an official performance by zama-ai here: cifar10.
And Concrete ML has other reference implementations, including GPT-2 LLM model.
Recent Breakthrough
- LUT (Lookup Table)
A method to reduce the amount of calculation by preparing a table in which the calculation f(x) is pre-calculated for all x in a certain range, and referring to the table when calculating. Jack, Gentry, Halevi, Platt proposed bit-wise based LUT in 2018, then, integer-wise based LUT, word-wise based LUT have been also proposed to modify it. - Programmable Bootstrapping
ZAMA proposed a technique to reduce noise to a fixed level while performing Evaluate in TFHE.
4. Example Use Cases
Secure Cloud Computing
Abstract: Executing programs and perform calculations on cloud computing over encrypted data
Benefits: Both on-premise and cloud computing options are available, even for systems that handle sensitive information such as personal data or information from other companies
Challenges and Discussion: Memory access patterns can reveal values, increasing costs, …
Example Researches: https://arxiv.org/pdf/1409.0829.pdf
https://arxiv.org/pdf/1409.0829.pdf
Prediction Market
Abstract: Prediction of stock price fluctuations based on sensors and cameras from IoT devices around the world
Benefits: Real-world data can be collected while protecting the privacy of passersby and others reflected in the IoT device.
Challenges and Discussion: Best Architecture is still under research, Performance, …
Example Researches: https://ieeexplore.ieee.org/document/10127502
https://ieeexplore.ieee.org/document/10127502
Medical Diagnostics
Abstract: Medical diagnoses such as cancer tests without leaking the patient's genetic sequence or radiographs to the server.
Benefits: Facilitates model collaboration between hospitals
Challenges and Discussion: Accuracy of analysis, to ensure that the intended privacy is truly protected, …
Example Researches: https://link.springer.com/chapter/10.1007/978-3-030-24202-2_8
5. Practices on Implementation
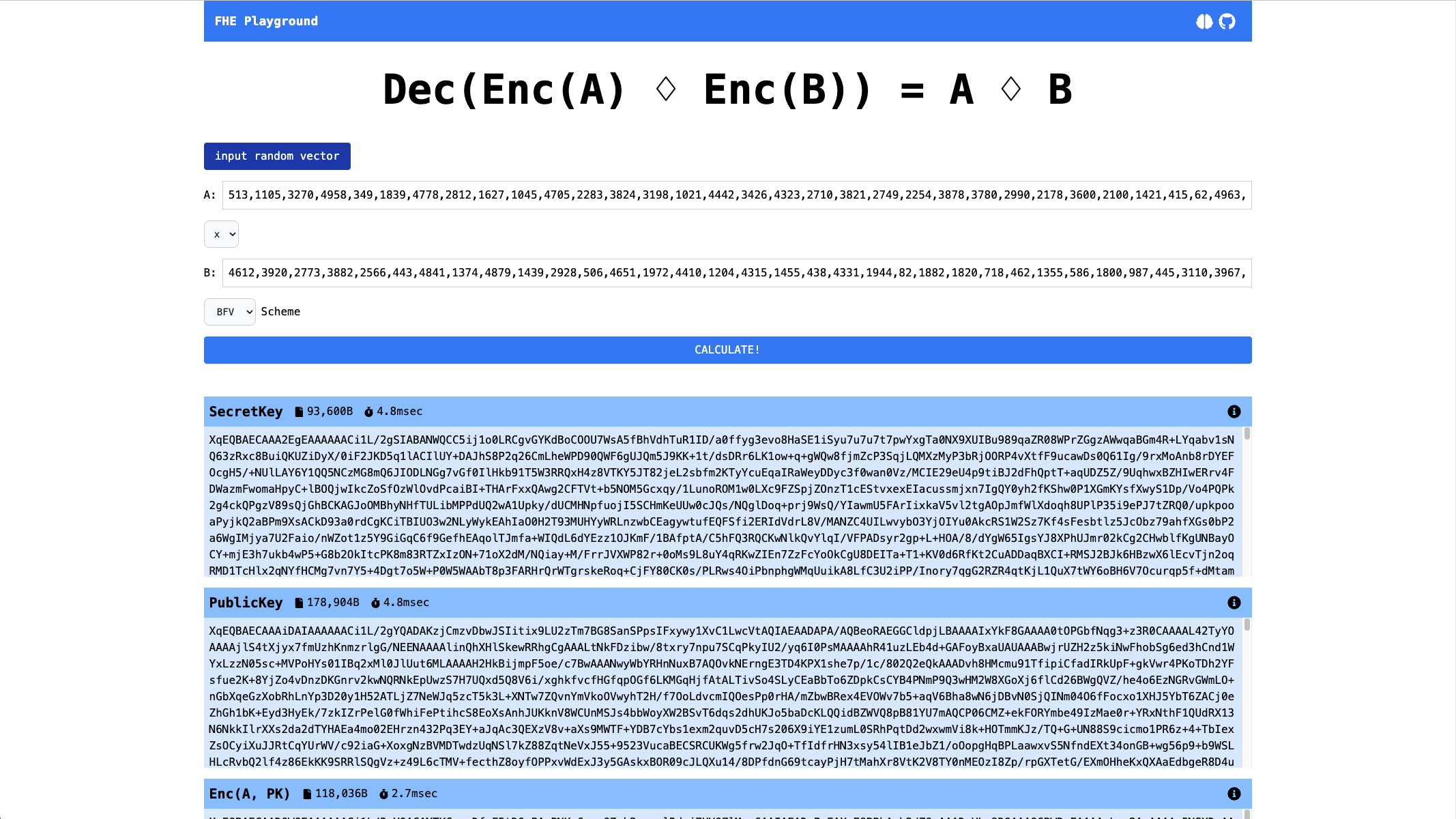
Practice in SEAL (through FHE Playground)
I built an app “FHE Playground” which you can try&learn FHE scheme easily on web. In this app, you can try add/mul operations with a pair of any vector inputs.
In the result, you can see each intermediate results to make sure FHE workflow step by step.
You can also check mathematical explanations for each step to learn about the methods in theory.
This app calls Microsoft/SEAL in the backend, which is a major FHE library now. As you can see the result, encryption/evaluation take less than 10ms. On the other hand, the data size is around 100kB.
In the SEAL library, you need to set those security parameters at first. Since those parameters affect to plaintext/ciphertext space, the values must be large enough to decrypt the correct values.
const securityLevel = seal.SecurityLevel.tc128;
const polyModulusDegree = 4096; // t: polynomial modulus
const bitSizes = [36, 36, 37]; // bit-length of the primes , at most 60 bits
const bitSize = 26;
Practice in concrete-ml (through FHE-ML Playground)
I also built “FHE-ML Playground” which recognizes the handwritten numeral. You can also check how it works step by step. (This app is little bit more complicated due to the library implementation though.)
This app calls FastAPI (fhe-ml-fastapi) which uses zama-ai/concrete-ml, the fastest TFHE compiler. You need to compile the FHE circuits in advance.
The secure inference takes almost 10sec and the data size is around 218kB.
I describe some practices from my experience below:
First, concrete-ml supports only Quantized Model because TFHE scheme can’t treat with the float values. Thus, the model must be constructed through QAT (Quantization Aware Training) by using library such as https://github.com/Xilinx/brevitas.
Second, there’s still lack of the client-side api. The app currently can’t encrypt/decrypt on the client-side, so it passes the raw data to FastAPI and encrypt/decrypt on the server-side. (The doc says that we could build both client/server side code on the deployment.)
Third, for the model tuning, users need to adjust parameters such as rounding. Currently, such properties affects the tradeoffs in accuracy and efficiency. So, You need to set the best number for your app requirement.
Forth, accuracy may vary depending on the task of the model. Testing of many types of models, such as image recognition, time series analysis, and generative models, is considered a future task, and it is quite possible that there may be missing parts in real-world use cases.
6. Future Works
Open Researches
- Verifiable FHE
When calculating FHE, if one wants to prevent servers from tampering with the result by intentionally adding values, the combination with zkSNARK is being considered for verifiability. For instance, zama proposed a method combining Plonky2 to prove the FHE bootstrapping in 20 minites. Or authentication-based methods like KeyedFHE are also under researches. - Hardware Acceleration
CPUs and memories suitable for FHE calculations are also being researched. - Hybrid Model (MPC/TEE)
Hybrid models in which only calculations that are too heavy for FHE (exponent, sin, etc.) are computed covertly by MPC or TEE have also been researched. Currently, it is known that the performance of the hybrid model is superior to that of FHE alone. - Application
In fact, research is underway to apply FHE to real use cases such as genome confidentiality computation and financial transactions as I already showed in Chapter 4.
Potential Applications
- Confidential Ethereum Block Building
Block Proposer outsources the building-block and generating KZG commitment to Block Builder without disclosing transactions. - Gaming
Incomplete Information Fully-onchain Game like Onchain Poker. - HPC/AI-specific Cloud Computing
- Business-to-business data collaboration
- National Defense
Detecting Log access from North Korean hackers, Confidential Satellite Analysis, and so on.
Social&Legal Considerations
- Currently, the law requires that even encrypted data should be managed in the same way as privacy information. This requires that the FHE ciphertext be stored in the device area, which requires a very large storage.
- Key management issues common to all wallets and public key cryptosystems arise; FHE's key size is particularly large, making it a significant problem.
Conclusion
The article provides an in-depth look at Fully Homomorphic Encryption (FHE), from its inception in 1978 to the development of various schemes enhancing its practicality. It outlines the basic principles of FHE, including its reliance on Lattice-based Cryptography, the concept of adding noise to encrypted data, and the importance of the bootstrapping technique to manage noise and maintain decryption integrity. The piece aims to enhance understanding of FHE's potential, offering practical examples and implementation insights.
FHE's significance lies in its ability to perform complex computations on encrypted data without ever decrypting it, thereby preserving data privacy. This capability is paramount for secure data analysis and processing in various industries, including healthcare and finance, where confidentiality is crucial. The future potential of FHE includes enabling secure cloud computing where sensitive data can be processed without exposing it to third-party service providers, thereby enhancing privacy and security in the digital age.