はじめに

先日PSE主催のMPC/FHE Residencyに参加してきました。2週間六本木で同じコワーキングスペースに集まり、MPCやFHEに関する最新の論文やライブラリについて紹介し合っていました。僕は6月からenricoとnamといっしょに取り組んでいるgridlockというプロジェクトを引き続き進めていて、最近の成果を論文として投稿したり、また別のアルゴリズムを実装したりしていました。最終的にもっと良い完成形が見えるところまで煮詰めていくことができました。

EDCONのサイドイベントではMPC & FHE Primerというのもやりましたが「MPC/FHEの実用例ってどんなのがあるの？」というのが気になっている人が多いようだったので、僕がgridlockと修士課程で研究している「秘密計算の数理最適化への応用」をここでも話そうと思います。ちなみにEthereum Meetupなどで何度か話したことがあります。今後もzkTokyoとかで機会があれば話すかもしれません。

数理最適化とは

世の中には色んな複雑な問題で溢れています。例えば、遠足のおやつを300円まで(しかしバナナはおやつには含まれない)に抑えるための最も満足度の高い組み合わせを選ぶとかですね。数理最適化とは、こういう現実の問題を数式として定式化する手法です。たとえば遠足の例だと、おやつの定価をx、満足度をyとしたときに、\sum x ≤ 300という制約の元で\sum yを最大化するといったふうになります。この\max \sum yを目的関数といいます。こうして定式化することによってアルゴリズムによって効率的に答えを求めることができます。

これは本当にいろいろな現実の問題にフォーカスしています。代表例としていくつかまとめた例を挙げます。

問題	説明	応用例
ナップサック問題	ナップサックの中に入る重量の範囲で、いくつかの品物を詰め込み入れた品物の総価値を最大にする問題	トラックの積載計画
投資ポートフォリオの選択
巡回セールスマン問題	セールスマンがいくつかの都市を1度ずつすべて訪問して出発点に戻ってくるときに、移動距離が最小になる経路を求める問題	電子回路の設計
医療サプライチェーン
Amazonの配達計画
工場の生産工程設計
最小費用流問題	出発地から目的地まで最小の費用で移動する経路を決める問題	カーナビのルート探索
インターネットのルーティング

そして、数理最適化はグラフ理論とも関係しています。インターネットのルーティングではルーターをノードとしたグラフで表すことがよくあるからです。グラフ理論のほうがなんとなくイメージしやすくてカッコいいので、たまにグラフ理論をベースに説明したりしています。

数理最適化と秘密計算

数理最適化ではプライバシーが必要となる場面は多々あります。たとえばルーティングでは、お互いのルーターの動作系(マシンスペックや位置など)を明かしてしまうとサイバー攻撃の対象になり得ます。サプライチェーンでは、どのサプライヤーからどの部品をどれだけ調達しているかは企業の競争力に直結するため、機密情報として扱われます。この情報が漏洩すると競合他社に有利な情報を与えることになりかねません。たとえ漏洩しなかったとしても、その情報を価格交渉の材料にされる可能性があります。

そしてそれらのケースで特に問題なのは、グラフの内容をサービス提供者や政府などの誰かに明かす必要があるということです。そうすると、各参加者から信頼されてそれらの情報を預かることもリスクになります。当然預かる企業のサーバーは攻撃の的になるわけなので、セキュリティ要件も500倍くらい上がります。結果として参加する企業が少なくなると最適化の効果が薄れてしまいます。

そこで、自分たちのデータは自分たちだけが知っていて、最適化の際に誰かを信頼して開示する必要がなくなればどうでしょうか。そうすれば、信頼する側もされる側もリスクをヘッジすることができて、より多くの企業はそのネットワークに参加することができるので、最適化の効果もより大きくなります。たとえ競合であっても、互いに情報を与えなければ協力しあうことだってできるかもしれません。

データを暗号化したまま計算を実行する秘密計算もまさにそんな世界を夢見ています。今まではAIやデータ解析が応用分野の中心でしたが、数理最適化のような現実の課題にもフォーカスできるようになれば、もっと可能性が広がるでしょう。

そして加速社会へ

私たちがgridlockというプロジェクトで取り組んでいるのはマルチラテラル・オブリゲーション・ネッティング（以下ネッティング）です。まずネッティングとはなんでしょうか(Google検索結果)。

たとえば何人かで旅行に行ったとき、領収書を持ち合って１つずつ清算するのではなく、合計額からなるべく相殺してから清算しますよね？そのほうが効率的ですから。

ネッティングはそれを企業や銀行の債務でおこなう決済方法をいいます。企業は請求書を信頼機関(政府など)に提出し、信頼機関は月に一回それぞれの企業の請求書や債権をもとに金額を相殺します。そして、各企業は相殺後の請求書を受け取ります。

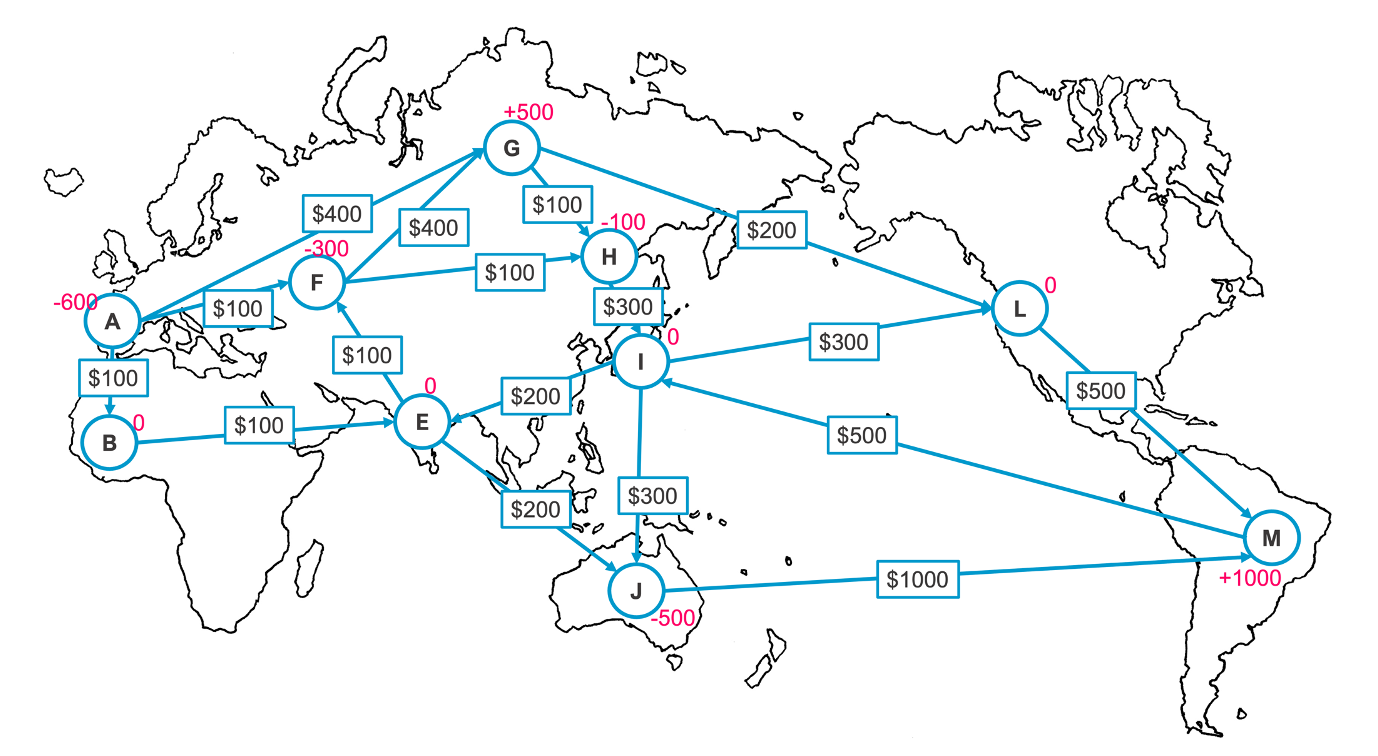
ネッティングは、請求書の金額をフロー、決済手数料をコストとおき、フローコストの総和を最小化する最小費用流に変換することで効率的に実行できます。

ネッティングをおこなうことで、送金コストを削減したり、システミックリスクを低減したり、流動性要件を緩和するといったメリットがあります。実際にスロベニアでは、GDPの1~7.5%もの金額を相殺しています[1]。これはおよそ最大700億円ほどを意味しますが、スロベニアは日本の1/70ほどのGDPなので、日本だと4.9兆円ほどの規模になります。

しかし、スロベニアでは各企業が政府に請求書を提出する必要があります。それがネックとなり、ネットワークへの参加率は1.2~8.3%に留まっています。そこでプライベートネッティングの出番となります。請求書の内容を隠したままネッティングを行なうことができて、参加率が50%に上がれば、相殺額は700億円から4200億円になり、日本だと30兆円ほどの規模になります。さらに、企業間だけでなく、消費者の生活品の購入や投資などもまとめてネッティングできるようになります。

これは明らかに経済活動を加速させます。企業は、受注が決まるとすぐに必要な人員を雇用したり物資を購入することができます。人々は、仕事が決まるとすぐに服や食事を買うことができます。着金するまで待ったり、銀行に説明して融資を受けにいく必要はなくなります。キャッシュフローの課題を緩和することで物事を前に進めやすい社会をつくることができます。

なにより素敵なのは、この社会をみんなの協力によってつくれるという点です。色んな企業や人がネットワーク・エコシステムに参加すればするほどその利益は大きくなっていきます。ネットワークの勝者のみが利益を享受するゼロサムゲームとは違います。これはEthereumが掲げるInfinite Gardenと同じ思想です。

関連研究

プライベートネッティングの関連研究には[2,3,4,5]などがありますが、いずれもMPCを用いたアルゴリズムが中心となっています。特に[5]はダブルスケーリング法を用いた効率的なアルゴリズムで、著者はライトニングネットワークのrebalanceへの応用も提案しています。

僕らの研究方針は、単体法などのより効率的な最適化アルゴリズムを採用したり、FHEやTEEなどの他の秘密計算技術と組み合わせたり、グラフ分解などのアイデアを適用して並列化したりすることです。

さいごに

研究に協力・応援してくれる人を大歓迎します。いつでもご連絡ください。

参考文献

1. Fleischman, T.; Dini, P. Mathematical Foundations for Balancing the Payment System in the Trade Credit Market. J. Risk Financial Manag. 2021, 14, 452. https://doi.org/10.3390/jrfm14090452
2. Toft, T. (2009). Solving Linear Programs Using Multiparty Computation. In: Dingledine, R., Golle, P. (eds) Financial Cryptography and Data Security. FC 2009. Lecture Notes in Computer Science, vol 5628. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-03549-4_6
3. Aly, A., Van Vyve, M. (2015). Securely Solving Classical Network Flow Problems. In: Lee, J., Kim, J. (eds) Information Security and Cryptology - ICISC 2014. ICISC 2014. Lecture Notes in Computer Science(), vol 8949. Springer, Cham. https://doi.org/10.1007/978-3-319-15943-0_13
4. Shahla Atapoor and Nigel P. Smart and Younes Talibi Alaoui. (2021). Private Liquidity Matching using MPC. Cryptology ePrint Archive, Paper 2021/475. https://eprint.iacr.org/2021/475
5. Avarikioti, Z., Pietrzak, K., Salem, I., Schmid, S., Tiwari, S., Yeo, M. (2022). HIDE & SEEK: Privacy-Preserving Rebalancing on Payment Channel Networks. In: Eyal, I., Garay, J. (eds) Financial Cryptography and Data Security. FC 2022. Lecture Notes in Computer Science, vol 13411. Springer, Cham. https://doi.org/10.1007/978-3-031-18283-9_17