This article is an output of what I learned through the Privacy and Scaling Explorations (PSE) Learning Grant Program. I am very grateful for such an opportunity. And I would like to express my gratitude to everyone at PSE who gave me feedback on writing the article.

Background

---

Many of the articles currently available explaining the MPC Wallet only go as far as explaining how the MPC Wallet functions from a high-level perspective. As a result, even users who are not familiar with software development or cryptography can understand what kind of concept the MPC Wallet is.

On the other hand, many misunderstandings arise among the general public because the explanations in these articles are vague.

Also, there are also many articles that exaggerate as if one proposal is vulnerable, in order to appeal that their proposal is superior.

In this article, we will help you correctly understand the MPC Wallet through detailed explanations about the technology in order to dispel these misunderstandings.

Introduction

---

The True Identity of MPC Wallet is "Threshold Signature"

What is often referred to as MPC Wallet in public, is actually a technology known as Threshold Signature.

The history of threshold signatures dates back to 1987[1]. The underlying Threshold Cryptography is a method that allows for the signing and encryption of messages in a situation where keys are distributed among several parties. To put it more bluntly, it's not about carefully managing one key, but rather having one key and multiple key-shares so it's okay if one of the share is leaked.

Particularly, Threshold ECDSA is attracting attention among threshold signatures, and the reason is obviously Bitcoin and Ethereum. Many blockchains adopt ECDSA signatures as their signature algorithm, and signatures are required to execute a transaction. Blockchains also have the property of having no key lifecycle because the account address is deterministically determined by the public key, and financial damage of Hundreds of millions of dollars can occur instantaneously due to the key's criticality.

By the way, it only recently started to be called MPC Wallet, and in an article by ZenGo in November 2019, it was referred to as "Threshold Wallet". Indeed, the term MPC Wallet feels more familiar, but it is an abstract term, and it is a word that can give users the impression of "I don't really understand, but it seems somehow safe".

Related Works on Threshold ECDSA

The first proposal of threshold signatures is Gennaro's Threshold DSS Signature (1996)[2], which uses Pedersen's Verifiable Secret Sharing.

MacKenzie and Reiter (2004)[3] proposed a two-party protocol.

Lindell et. al.(2017)[4] proposed a practical protocol that improved MacKenzie's protocol. Later, they extended it to a multi-party protocol (2018)[5].

Many of these methods have used Paillier Encryption or Oblivious Transfer.

Recently, IntMax Wallet has released an FHE-based MPC Wallet. In addition, Coinbase announced Wallet as a Service.

Honest Majority vs Dishonest Majority

In (t, n) threshold signatures, a signature can be restored when t signature shares are collected from n people.

An Honest Majority is a protocol in which more than n/2 of the participants perform their calculations honestly, when n ≥ 2t+1.

A Dishonest Majority is a protocol where there is a possibility that more than n/2 of the participants may not perform their calculations honestly, when n-1 > t. In a Dishonest Majority, it is necessary to verify the values sent by each party every time.

Preliminaries

---

1. ECDSA Signature

The flow of performing an electronic signature on a message m by ECDSA is shown below.

Sign(x, m):

1. random k \stackrel{\}{\leftarrow} \mathbb{Z}_{p}$
2. R = g^k mod p
3. r = H(R)
4. s = k^{-1}(m+rx) modp
5. \sigma = (r,s)

2. Additive Homomorphic Encryption

When there are two messages m_1,m_2, Additive Homomorphic Encryption is a type of encryption that satisfies E(m_1+m_2)=E(m_1)+E(m_2). Examples include Paillier Encryption based on RSA encryption and Lifted ElGamal based on ElGamal encryption. Below is an example of Paillier Encryption.

KeyGen:

1. from prime number p,q, n=pq
2. \lambda = LCM(p-1, q-1)
3. g \stackrel{\}{\leftarrow} \mathbb{Z}_{n^2}$
4. \mu = (L(g^{\lambda }mod n^2))^{-1} modn
   • s.t. L(x)=\frac{x-1}{n}
5. pk = (n, g), sk = (\lambda, \mu)

Enc:

1. r \stackrel{\}{\leftarrow} \mathbb{Z}_{n^2}$
2. c = g^mr^n modn^2

Dec:

1. m = L(c^{\lambda}modn^2)\times\mu modn

3. MtA Protocol

It is a method of converting a multiplicative share k= a_1a_2 to an additive share v=b_1+b_2 without revealing each other's share. Known methods include the Paillier method, the Castagnos-Laguillaumie method, and the OT method. The following figure shows an example of the Paillier method.

https://eprint.iacr.org/2023/1312.pdf

4. Commitment Scheme

It guarantees that the value has not been changed afterwards. There are two characteristics: binding and hiding. Mainly, ElGamal Commitment and Pedersen Commitment are mentioned. An example of Pedersen Commitment is shown below.

Commit(a):

1. group element g, h
2. random r \stackrel{\}{\leftarrow} \mathbb{Z}_{n^2}$
3. commitment C = g^ah^r

5. Trapdoor Commitment Scheme

It is about the Commitment Scheme that is information-theoretically secure (satisfies Non-malleability). The probability that an attacker with infinite computational resources succeeds to distinguish that committed message and the random number is negligible.

6. Secret Sharing

This refers to a method of generating a key share that can restore the private key when n are gathered, and distributing it to n parties. The administrator who generates the key and key shares is called a Dealer.

The simplest way is as follows. First, the dealer generates a random t-1 degree polynomial p(x). Next, calculate p(i) for all 1≤i≤n, and share it with the party as a share.

Ditributed Key Generation (DKG)

However, there are issues with this method depending on the situation. The problem lies in the fact that the dealer knows the private key. If the dealer has malicious intent, they can leak the private key to someone. Or, if the key sharing was eavesdropped on by an adversary, the private key may be leaked even if the key share was securely shared. The solution to this is Distributed Key Generation (DKG). With DKG, you don't need a dealer, and the key share can be generated by the party.

Verifiable Secret Sharing (VSS)

However, there is still a problem. The point is that you cannot verify whether the key share received by the party is a share that can restore the private key when t pieces are gathered. The solution to this is Verifiable Secret Sharing (VSS). In VSS, by publishing the commitments of each coefficient of the polynomial that can restore the private key, you can verify whether the key share you generated is included in the points on the polynomial. This can prevent malicious dealers and parties from using fraudulent key shares. VSS is known for methods such as Feldman and Benaloh, and there are also AVSSs that can execute VSS asynchronously. An example of the Feldman method is given below. The Feldman method is very simple, but be careful as it cannot verify that it is t-consistant alone.

share:

1. p(x)=\sigma + a_1x + a_2x^x + \cdots + a_tx^t modq
   • sk = \sigma
2. open C_0 = g^{\sigma}
3. open C_1 = g^{a_1}, \cdots , C_t = g^{a_t}
4. send p(i) to parties P_i

verify:

1. check if g^{p(i)} = \prod_{j=0}^{t}C_j^{i^j}

Overview of Threshold ECDSA

---

To calculate the signature share \sigma_i, You need to obtain k, R by multi-party computation.

The following is a summary of the various methods of Threshold ECDSA. In the Dishonest Majority, Paillier Encryption and Obvious Transfer are trade-offs in computation and communication.

	Computation Cost	Communication Cost	Party Majority
Shamir Secret Sharing	Low	Low	Honest
Paillier Encryption	High	Low	Dishonest
Oblivious Transfer	Low	High	Dishonest

Honest Majority Protocol

---

First, to understand the protocol of Threshold ECDSA, we introduce a relatively simple Honest Majority Protocol.

1. Fast Threshold ECDSA with Honest Majority[11]

The method proposed by Ivan et. al. in 2020, uses Shamir Secret Sharing. This proposal has also been adopted in the PoC of Ledger Nano S. Although there are constraints such as not being applicable to 2-out-of-2 or requiring all participants to be online, it is a simple algorithm. The flow of this method's signature is shown below.

In this method, Joint Random Secret Sharing is used for generating shares of x_i and k_i. Joint Random Secret Sharing is a technique to generate shares x_i without informing each other of the secret value x.

KeyGen:

1. generates x_i using Joint Random Secret Sharing
2. y_i = g^{x_i}
3. sends y_i to other parties
   1. f: t-degree polynomial for y_i
4. computes y = f(0) = g^x

Sign:

1. generates k_i using Joint Random Secret Sharing
   1. reveals R = g^k
2. computes k^{-1}_i using Beaver’s Inversion Trick Protocol
   1. computes a random a_i
   2. broadcasts w_i = a_ik_i
      1. f_w: t-degree polynomial for w_i
   3. computes w = f_w(0)
   4. computes k_i^{-1} = a_i \cdot w^{-1}
3. s_i = k^{-1}_i(m+rx_i)

In this method, it becomes impossible to verify whether the w_i sent from each party is really correct, and when t or more parties collude to send values from a different polynomial, it is possible to generate a wrong signature. Therefore, it is necessary for the majority of participants to perform calculations honestly, at least with n≥2t+1.

Dishonest Majority Protocol

---

Next, I will introduce two protocols that work even if more than half of the participants are dishonest.

1. GG18[6]

The first Malicious Model inspired by Threshold ECDSA from ECDSA Assumptions, and is now one of the mainstream. It is called GG18, taking the initials of the proposers Gennaro and Goldfeder (both very famous cryptographers) and the AD in which the paper was presented. This method uses the Trapdoor Commitment Scheme, Feldman’s VSS, Paillier Encryption, MtA Protocol. It is used in implementations such as Coinbase, Binance, ZenGo. The algorithm of GG18 is shown below.

KeyGen:

1. P_i selects u_i \stackrel{\}{\leftarrow} \mathbb{Z}_{p}$
   1. P_i computes [KGC_i, KGD_i] = Com(g^{u_i})
      • Com: Trapdoor Commitment Scheme
   • broadcasts KGC_i
   1. broadcasts E_i
      • E_i: Paillier’s pk
2. P_i broadcasts KGD_i
   1. decommit y_i = g^{u_i}
   2. x_i = VSS(u_i)
      1. VSS: Feldman-VSS Protocol
      • x_i: Shamir Secret Sharing
   3. pk: y = \sum_{i}y_i , sk: x = \sum_{i}u_i
   4. X_i = g^{x_i}
3. N_i = p_iq_i
   1. prove in ZK that
      1. he knows x_i using Shnorr Protocol
      2. N_i is square-free using proof of Gennaro, Micciancio, and Rabin

Sign(m):

1. P_i selects k_i,\gamma_i \stackrel{\}{\leftarrow} \mathbb{Z}_{p}$
   1. k = \sum k_i , \gamma = \sum \gamma_i (mod p)
   2. k\gamma = \sum k_i\gamma_i , kx = \sum k_iw_i (mod p)
   3. P_i computes [C_i, D_i] = Com(g^{\gamma_i})
   4. P_i broadcasts C_i
      • binds \gamma_i to prevent changing afterwards
2. P_i, P_j engages in two MtA additive share conversion subprotocols
   1. run MtA protocol with shares k_i\gamma_j = \alpha_{ij} + \beta_{ij}
      • P_i sets \delta_i = k_i\gamma_i + \sum_{j\neq i}\alpha_{ij} + \sum_{j \neq i}\beta_{ji}
      • \delta_i: additive share of k\gamma
   2. run MtA protocol with shares k_iw_j = \mu_{ij} + \nu_{ij}
      • P_i sets \sigma_i = k_iw_i + \sum_{j \neq i}\mu_{ij} + \sum_{j \neq i}\nu_{ji}
      • \sigma_i: additive share of kx
3. P_i broadcasts \delta_i
   1. reconstructs k\gamma
   2. computes (k\gamma)^{-1} mod p
4. P_i broadcasts D_i
   1. decommit \Gamma_i = g^{\gamma_i}
      • proves ZK that he knows \gamma_i s.t. \Gamma_i = g^{\gamma_i} using Schnorr Protocol
   2. R = [\prod_{i \in S}\Gamma_i]^{k\gamma^{-1}} = g^{k^{-1}} modp
   3. r = H(R)
5. P_i sets s_i = mk_i + r\sigma_i
   1. selects l_i,\rho_i \stackrel{\}{\leftarrow} \mathbb{Z}_{p}$
   2. computes V_i = R^{s_i}g^{l_i} , A_i = g^{\rho_i} , [\hat{C}_i, \hat{D}_i] = Com(V_i, A_i)
      • commitment of s_i
      • l = \sum l_i , \rho = \sum \rho_i (mod q)
   3. P_i broadcasts \hat{C_i}
   4. P_i broadcasts \hat{D_i}
      • proves in ZK that he knows s_i, l_i, \rho_i
   5. V = g^{-m}y^{-r}\prod V_i = g^l
   6. A = \prod A_i
   7. P_i computes U_i = V^{\rho_i} , T_i = A^{\rho_i} , [\tilde{C}_i, \tilde{D}_i] = Com(U_i, T_i)
   8. P_i broadcasts \tilde{C_i}
   9. P_i broadcasts \tilde{D_i}
      • aborts if \prod [T_i] \neq \prod U_i
   10. P_i broadcasts s_i
   11. P_i computes s = \sum s_i
       • aborts if s is invalid signature

In phase5, if you simply share s_i, the protocol will fail if an adversary sends an invalid s_i, but this would only provide information about the signature to the adversary. To prevent this, a naive approach would be to first verify S_i = R^{s_i} like DSA signature verification, but this too would allow an adversary to fail the proof and only obtain information about S_i.

Therefore, in this proposal, we mask R^{s_i} further with a random number g^{l_i}, set V_i = R^{s_i}g^{l_i}, and then perform DSA signature verification on it. If we disclose g^{l_i}, we can remove the mask of R^{s_i}, so we add a step to calculate g^l after randomizing U = g^{l\rho} (in the manner of DH key exchange).

2. MPC-CMP[8]

MPC-CMP combines GG18 and the Lindell method, adding several features such as Proactive Key Refresh. It uses Paillier Encryption not only as a semi-homomorphic but also as a commitment scheme. As long as Paillier Encryption is semantic-secure, it can satisfy the characteristics of binding and hiding.

Pre-Sign(m):

1. Round1
   1. P_i selects k_i,\gamma_i \stackrel{\}{\leftarrow} \mathbb{F}{q}, \rho_i,\nu_i \stackrel{$}{\leftarrow} \mathbb{Z}{n}$
   2. sets G_i = enc_i(\gamma_i;\nu_i) , K_i = enc_i(k_i;\rho_i)
   3. computes \psi_{ji}^{0} = M(prove, \prod_J^{enc}, (sid, i), (L_{\epsilon},K_i);(k_i,\rho_i)) for every j≠i
      • prove in NK that he knows k_i s.t. enc_i(k_i) = K_i without disclosing k_i,\rho_i
   4. broadcasts (sid, i, K_i, G_i)
   5. send (sid, i, \psi_{j,i}) to each P_j
2. Round2
   1. verifies \psi_{ji}^{0}
   2. sets \Gamma_i = g^{\gamma_i}
   3. for every j ≠ i , sample r_{ij},s_{ij},\hat{r}_{ij} , \hat{s}_{i_j} \stackrel{\}{\leftarrow} \mathbb{Z}{n} , \beta{ij}, \hat{\beta}_{i_j} \stackrel{$}{\leftarrow} {J}$
      1. D_{ji} = (\gamma_i \odot K_j) \oplus enc_j(-\beta_{ij};s_{ij}) and F_{ji} = enc_i(\beta_{ij} ; r_{ij})
         • D_{ji}: enc_j(\gamma_ik_j - \beta_{ij})
         • F_{ji}: enc_i(\beta_{ij})
      2. \hat{D}_{ji} = (x_i \odot K_j) \oplus enc_j(-\hat{\beta}_{ij};\hat{s}_{ij}) and \hat{F}_{ji} = enc_i(\hat{\beta_{ij}} ; \hat{r}_{ij})
         • \hat{D}_{ji}: enc_j(x_ik_j - \hat{\beta}_{ij})
         • \hat{F}_{ji}: enc_i(\hat{\beta}_{ij})
      3. \psi_{ji} = M(prove, \prod_j^{aff_p},(sid,i),(L_{\epsilon},J_{\epsilon},{D}_{ji},K_j,F_{ji},G_i);(\gamma_i,\beta_{ij},s_{ij},r_{ij},\nu_i))
      4. \hat{\psi}_{ji} = M(prove, \prod_j^{aff_g},(sid,i),(L_{\epsilon},J_{\epsilon},\hat{D}_{ji},K_j,\hat{F}_{ji},X_i);(x_i,\hat{\beta}_{ij},\hat{s}_{ij},\hat{r}_{i,j}))
      5. \psi'_{ji} = M(prove, \prod_j^{log},(sid,i),(L_{\epsilon},G_i, \Gamma_i,g);(\gamma_i,\nu_i))
   4. sends (sid,i,\Gamma_i,D_{ji},F_{j_i},\hat{D}_{ji},\hat{F}_{ji},\psi_{ji},\hat{\psi}_{ji},\psi'_{ji}) to each P_j
3. Round3
   1. verifies \psi_{ij},\hat{\psi}_{ij},\psi'_{ij}
   2. sets \Gamma = \prod \Gamma_j , \triangle_i = \Gamma^{k_i}
   3. for every j \neq i , do:
      1. sets \alpha_{ij} = dec_i(D_{ij}) and \hat{\alpha} = dec_i(\hat{D}_{ij})
      2. sets \delta_i = k_i\gamma_i + \sum_{j≠i}\alpha_{ij} + \sum_{j≠i}\beta_{ij}
      3. sets \chi_i = k_ix_i + \sum_{j≠i}\hat{\alpha}_{ij} + \sum_{j≠i}\hat{\beta}_{ij}
      4. \psi''_{ji} = M(prove, \prod_j^{log},(sid,i),(L_{\epsilon},K_i, \triangle_i,\Gamma);(k_i,\rho_i))
   4. sends (sid,i,\delta_i,\triangle_i,\psi'') to each P_j
4. Output
   1. verifies \psi''
   2. verifies g^{\delta} = \prod \triangle_j
   3. sets R = \Gamma^{\delta^{-1}}

Sign(m):

1. sets r = H(R)
   1. and computes \sigma_i = k_im + r\chi_i
2. broadcasts (sid,i,\sigma_i)
3. verify \sigma

Is 8x Speedup Really True?

MPC-CMP enables digital asset transactions to be signed in just 1 round, meaning that it offers the fastest transaction signing speeds of any MPC algorithm by 800%.
https://www.fireblocks.com/what-is-mpc/

The Fireblocks release describes that MPC-CMP requires only one round of communication compared to GG18, which requires nine rounds, as "8x faster". However, this comparison is not appropriate.

In the MPC-CMP method, the secret computation of R is separated into a Pre-Sign protocol and the calculation of the signature share \sigma_i into a Sign protocol. The same can be done in the GG18 method, where phases 1 to 4 in the algorithm can be considered a Pre-Sign protocol instead of a Sign. Then, GG18's Sign:phase5 can be achieved in 5 rounds, so the correct number of rounds reduced is not 8 but 4 rounds.

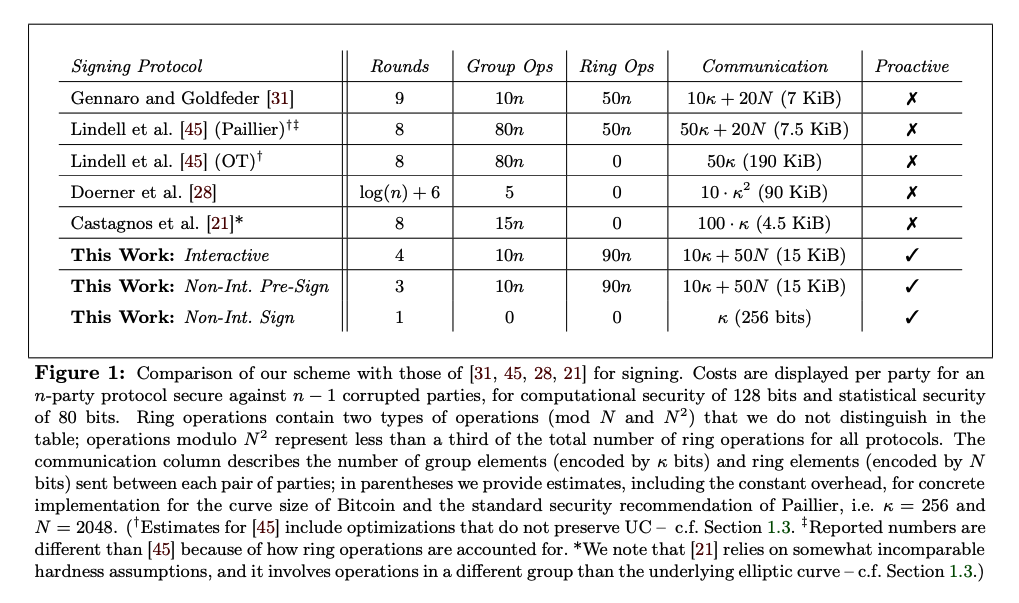
Furthermore, a reduction in rounds does not necessarily mean an increase in speed. Generally, the number of communications and the amount of calculation are in a trade-off relationship. Comparing the Pre-Sign of Gennaro and Goldfeder and This Work, the MPC-CMP has 40n more ring operations and the total amount of data required for communication is about twice as much. Furthermore, the number of zero-knowledge proofs required is also three more in MPC-CMP. In other words, the computational cost of MPC-CMP is higher.

Considering the above, claiming that “MPC-CMP is eight times faster” is an exaggeration. In order to confirm which is faster, it is necessary to compare them by implementation benchmarks under LAN/WAN communication.

https://eprint.iacr.org/2020/492.pdf

Security Analysis

---

Is UC-Security safer?

In this article by Fireblocks, it is stated that MPC-CMP only satisfies UC-security, and is therefore described as having the highest level of security in the industry.

UC-Security (Universally Composable Security) is a framework used for the design and analysis of cryptographic protocols. First, an Ideal Function is defined, which outlines the security requirements. Then, a Real World Protocol is defined, which determines the protocol that the attacker and participants execute. It is then proven that the attacker can achieve the Ideal Function in the Real World Protocol. Finally, it is demonstrated that this can be composed with other UC securities.

The table below shows the Ideal Function and Real World Protocol defined in the GG18 and MPC-CMP methods.

	GG18	MPC-CMP
Ideal Function	1. Authorized set of parties may generate a valid signature for any message.

2. Unauthorized set of parties cannot compute a valid signature for a message that has never been signed before. | 1. Authorized set of parties may generate a valid signature for any message.
3. Unauthorized set of parties cannot compute a valid signature for a message that has never been signed before. |
   | Real World Protocol | 1. the attacker controls t parties.
4. The attacker has access to a signature oracle for messages of his choice.
5. The attacker wins the game if he can generate a valid signature for a previously unsigned message. | 1. the attacker controls 1 party.
6. The attacker has access to a signature oracle for messages of his choice.
7. The attacker wins the game if he can generate a valid signature for a previously unsigned message.
8. The attacker can query the data (g^{k-1}) for a message-independent signature. |

Indeed, the UC-Security has not been proven in the GG18 method. However, as mentioned above, the safety of both has been proven at least. Rather, the Real World Protocol is more advantageous for the attacker in GG18. Therefore, it is not possible to say definitively which is safer.

Risk of Key Endangerment

While it has been proven that the mutual forging of signatures is impossible, the possibility of key share leakage has not been addressed. Therefore, there is a risk of giving away secret value information as parties execute the protocol.

In GG18, they were preventing the adversary from getting information about s_i in advance, but MPC-CMP does not prevent this, making it easier for the adversary to obtain information.

Identifiable Abort

In the derived proposal[7][9], an addition of a feature called Identifiable Abort, which can identify a malicious party when the protocol fails, is proposed. This allows to mitigate the above risks by banning any party that has ever performed a malicious execution.

Safety of Commitment

GG18 used the Trapdoor Commitment Scheme, but a similar commitment is achieved with Paillier Encryption and zero-knowledge proof. While the Trapdoor Commitment Scheme is an information-theoretically safe algorithm, zero-knowledge proof is a computationally safe algorithm.

Safety of Pre-Sign

In Groth's research[10], safety analysis of ECDSA's presignature is performed. At RWC2022, an attack and countermeasure against Threshold ECDSA have been proposed.

Assumptions in security proofs

The proposed method should note the following assumptions. If these assumptions are not followed, safety cannot be guaranteed.

• Parties are authenticated in a secure manner to participate
• A secure communication channel is established between parties

Attack methods using implementation bugs

In the attack method announced by ZenGo in 2020, three types of attack methods, "Forget-and-Forgive", "Lather, Rince, Repeat", "Golden Shoe" are introduced. "Forget-and-Forgive" is a method where Party C sends a malicious value only to B out of A and B in the key refresh phase, B aborts it but A accepts it and discards the old key share, permanently locking A's assets. The other two methods also restore the user's key share by using non-standardized cryptographic primitives or skipping verifications of proofs that should originally have integrity.

The Alpha-Ray Attack method announced by ZenGo in 2021 is a method where one party completely restores the secret key via running the signing protocol for several times by leaking one bit of the secret key in the MtA Protocol. This is an attack method limited to when the size of the Paillier secret key is small, but since most implementations did not verify the key size, the attacker was able to attack using a Paillier key with a small key size. Rosario, the author of GG18, explained that this bug was caused by a typo in the paper.

https://twitter.com/rgennaro67/status/1471147996226150401?s=20

The attack method called BitForge, discovered by Fireblocks in 2023, is a derivative of Alpha-Ray, and takes advantage of the fact that it doesn't check the factors of Paillier's public keys, allowing the attacker to use composite numbers for the keys p and q that should originally be prime numbers, and restore the secret key through several signatures.

All of the above attack methods are not attacks on the cryptographic protocol, but rather on the implementation flaws. It's important to be careful, as anything can be dangerous depending on how it's used.

MPC-CMP is a relatively new method and no such attack methods have been reported yet. However, attacks are often found over a span of 10 years, so continued caution is necessary.

Threshold ECDSA itself is also a new technology, with practical proposals only being made in 2018. Continued research is needed for users to be able to use it safely.

Reference

---

1. Desmedt, Y.: Society and group oriented cryptography: A new concept. In: Pomerance, C. (ed.) Advances in Cryptology - CRYPTO ’87, A Conference on the Theory and Applications of Cryptographic Techniques, Santa Barbara, California, USA, August 16-20, 1987, Proceedings. Lecture Notes in Computer Science, vol. 293, pp. 120–127. Springer (1987).
2. Gennaro, R., Jarecki, S., Krawczyk, H., Rabin, T.: Robust threshold DSS signatures. In: Maurer, U.M. (ed.) Advances in Cryptology - EUROCRYPT ’96, International Conference on the Theory and Application of Cryptographic Techniques, Saragossa, Spain, May 12-16, 1996, Proceeding. Lecture Notes in Computer Science, vol. 1070, pp. 354–371. Springer (1996).
3. MacKenzie, P.D., Reiter, M.K.: Two-party generation of DSA signatures. Int. J. Inf. Sec. 2(3-4), 218–239 (2004).
4. Lindell, Y.: Fast secure two-party ECDSA signing. In: Katz, J., Shacham, H. (eds.) Advances in Cryptology - CRYPTO 2017 - 37th Annual International Cryptology Conference, Santa Barbara, CA, USA, August 20-24, 2017, Proceedings, Part II. Lecture Notes in Computer Science, vol. 10402, pp. 613–644. Springer (2017).
5. Lindell, Y., Nof, A.: Fast secure multiparty ECDSA with practical distributed key generation and applications to cryptocurrency custody. In: Lie, D., Mannan, M., Backes, M., Wang, X. (eds.) Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, CCS 2018, Toronto, ON, Canada, October 15-19, 2018. pp. 1837–1854. ACM (2018).
6. Rosario Gennaro and Steven Goldfeder. 2018. Fast Multiparty Threshold ECDSA with Fast Trustless Setup. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security (CCS '18). Association for Computing Machinery, New York, NY, USA, 1179–1194.
7. Rosario Gennaro and Steven Goldfeder, One Round Threshold ECDSA with Identifiable Abort in Cryptology ePrint Archive, Paper 2020/540, 2020.
8. Ran Canetti and Nikolaos Makriyannis and Udi Peled, UC Non-Interactive, Proactive, Threshold ECDSA in Cryptology ePrint Archive, Paper 2020/492, 2020.
9. Ran Canetti and Rosario Gennaro and Steven Goldfeder and Nikolaos Makriyannis and Udi Peled, UC Non-Interactive, Proactive, Threshold ECDSA with Identifiable Aborts, in Cryptology ePrint Archive, Paper 2021/060, 2021
10. Groth, J., Shoup, V. (2022). On the Security of ECDSA with Additive Key Derivation and Presignatures. In: Dunkelman, O., Dziembowski, S. (eds) Advances in Cryptology – EUROCRYPT 2022. EUROCRYPT 2022. Lecture Notes in Computer Science, vol 13275. Springer, Cham.
11. Damgård, I., Jakobsen, T.P., Nielsen, J.B., Pagter, J.I., Østergaard, M.B. (2020). Fast Threshold ECDSA with Honest Majority. In: Galdi, C., Kolesnikov, V. (eds) Security and Cryptography for Networks. SCN 2020. Lecture Notes in Computer Science(), vol 12238. Springer, Cham.